Реферат: Спектри і спектральний аналіз
![]() .
.
Якщо в цьому співвідношенні перейти від комплексних спектрів до їх модулів, то одержимо
![]() ,
,
тобто при запізнюванні – чи взагалі при зсуві функції за шкалою часу спектр її залишається незмінним. Інакше кажучи, спектр не залежить від вибору початкового моменту для відліку часу.
Наступна теорема відноситься до транспозиції (переносу) спектрів. Питання ставиться в такий спосіб: якій функції відповідає спектр, зміщений за шкалою частот по ![]() ?
?
Оскільки
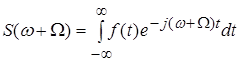 ,
,
то, отже, комплексний спектр вихідного виду буде властивий функції
![]() .
.
Слід зазначити одну цікаву обставину. Застосовуючи розкладання Фур'є, ми маємо справу з парою перетворень Фур'є.
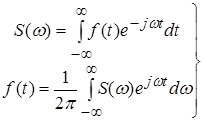 .
.
У цих формулах привертає увагу те, що час ![]() і кругова частота
і кругова частота ![]() входять у них симетрично. Формули можуть бути зроблені цілком симетричними, якщо, змінивши визначення, рознести множник
входять у них симетрично. Формули можуть бути зроблені цілком симетричними, якщо, змінивши визначення, рознести множник ![]() на два інтеграли (тобто ввести в обох формулах множник
на два інтеграли (тобто ввести в обох формулах множник ![]() ), що часто і роблять.
), що часто і роблять.
3. Поточний спектр
За основним визначенням спектральна щільність виражається формулою
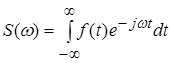 .(4)
.(4)
Таким чином, для знаходження спектра необхідно виконати інтегрування за часом у нескінченних межах. Це можливо, якщо функція ![]() відома на всьому нескінченному відрізку осі часу. Але якщо функція
відома на всьому нескінченному відрізку осі часу. Але якщо функція ![]() є відображення деякого реального фізичного процесу, що є об'єктом нашого спостереження, і якщо весь хід цього процесу не може бути чітко передбачений на підставі теоретичних розумінь, то відомості про функцію
є відображення деякого реального фізичного процесу, що є об'єктом нашого спостереження, і якщо весь хід цього процесу не може бути чітко передбачений на підставі теоретичних розумінь, то відомості про функцію ![]() ми одержуємо лише в результаті наших спостережень. Наприклад, ЕЕГ має досить коротку довжину в часі. Тому ми можемо виконати інтегрування не в нескінченних бокових границях, як цього вимагає визначення (4), а лише до необхідного поточного моменту.
ми одержуємо лише в результаті наших спостережень. Наприклад, ЕЕГ має досить коротку довжину в часі. Тому ми можемо виконати інтегрування не в нескінченних бокових границях, як цього вимагає визначення (4), а лише до необхідного поточного моменту.
Інтегрування може бути виконане в межах від ![]() до поточного часу
до поточного часу ![]() . Змінене в такий спосіб визначення спектра набуде виду
. Змінене в такий спосіб визначення спектра набуде виду
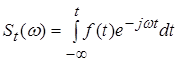 .(5)
.(5)
Величина ![]() , що є функцією не тільки частоти, але й часу, називається поточним спектром.
, що є функцією не тільки частоти, але й часу, називається поточним спектром.
У даних умовах спостереження процесу (чи сам процес) фактично може починатися в деякий момент ![]() , що знаходиться в минулому на кінцевому віддаленні від поточного моменту
, що знаходиться в минулому на кінцевому віддаленні від поточного моменту ![]() . У цьому випадку момент
. У цьому випадку момент ![]() може бути прийнятий за початок відліку часу, і ми можемо визначити поточний спектр у такий спосіб:
може бути прийнятий за початок відліку часу, і ми можемо визначити поточний спектр у такий спосіб:
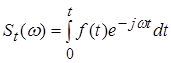 . (6)
. (6)
Ми надалі користуватимемося останнім визначенням спектра.
Зрозуміло, що пов'язування математичного визначення спектра з умовами реального експерименту само по собі має велике значення. Поняття поточного спектра є взагалі дуже плідним.
Ми розпочали викладання теорії спектрів зі спектра періодичної функції, що визначається співвідношенням ![]() .
.
Періодична функція є математичною абстракцією. Ця абстракція дуже корисна. Але треба мати на увазі, що не може існувати ніякого реального фізичного процесу, що відповідає визначенню (2). Будь-який дійсний процес має початок і кінець, і, отже, описується виразом виду (1) лише протягом кінцевого відрізку часу. Ми називаємо дійсний процес, що циклічно повторюється, періодичним, якщо цей процес триває досить довго. Мірилом тривалості є кількість періодів; тривалість велика, якщо кількість періодів набагато більше одиниці. Якщо взяти короткий відрізок процесу, то він зовсім не матиме періодичного характеру. Періодичність процесу виявляється не відразу; лише з часом виявляються характерні риси процесу. Поточний спектр саме й виражає зі спектральної точки зору цей розвиток процесу.
Спектр короткого відрізка процесу – за невеликий час від його початку – однорідний, оскільки короткий відрізок будь-якого процесу є просто коротким імпульсом. Якщо надалі відбувається періодичне повторення деякого циклу явища, то на поточному спектрі починають формуватися максимуми на основній частоті та її гармоніках. Ці максимуми стають все більш гострими і високими, а значення спектральної щільності в інтервалі між максимумами зменшується і – лише в границях, при ![]() , – суцільний поточний спектр вироджується в лінійчастий спектр періодичного в точному розумінні процесу.
, – суцільний поточний спектр вироджується в лінійчастий спектр періодичного в точному розумінні процесу.
Зазвичай при досить великих тривалостях процесу максимуми робляться настільки вузькими, що їх можна вже трактувати практично як лінії. Однак це не применшує принципового значення всього сказаного вище – періодичний процес є лише метою, до якої може прагнути з часом реальний процес, що повторюється.
Для з'ясування висловлених розумінь побудуємо поточний спектр синусоїди. Застосовуючи визначення (6) і підставляючи в нього ![]() , знайдемо
, знайдемо
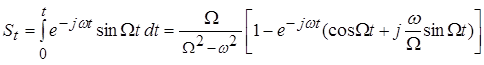 .(7)
.(7)
Формулу (7) можна значно спростити, розглядаючи значення спектральної щільності для дискретних моментів