Реферат: Спектры непериодических сигналов

Пусть задан сигнал в виде ограниченной во времени функции s(t), отличной от нуля в промежутке t₁ t₂ . Выделим произвольный отрезок времени T, включающий промежуток t₁ t₂ , далее продолжим аналитически s(t) на всю бесконечную ось с периодом T. Тогда мы сможем разложить такую периодическую функцию s(t) в гармонический ряд Фурье. В комплексной форме будем иметь:

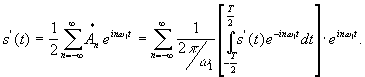
Полученный ряд на участке t₁ t₂ будет точно соответствовать нашей функции s(t). Однако, если нас интересуют моменты времени за участком t₁ t₂ , то необходимо увеличить период Т, т. е. отодвинуть повторные значения функции s(t). Производя замену переменных и переходя от суммирования к интегрированию, получим

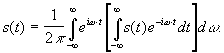
где

- спектральная плотность сигнала s(t).

Спектр непериодического сигнала сплошной (непрерывный) и распространяется на отрицательные частоты.

Если , то - модуль спектральной плотности – амплитудно-частотная характеристика.

- фазово-частотная характеристика.

Необходимое условие существования спектральной плотности

Пример. Спектр прямоугольного сигнала

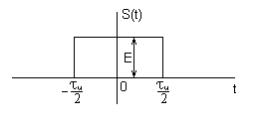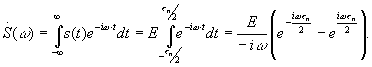
Согласно формуле Эйлера

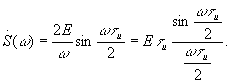
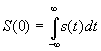- площадь под импульсом.

1.1 Свойства преобразования Фурье

а) Сдвиг сигнала во времени s₂ (t)=s₁ (t-t₀ ).

Сдвиг во времени функции s(t) на ±t₀ приводит к сдвигу фазы спектра на ±wt₀ . Это позволяет для удобства разложения в спектр сдвигать сигнал относительно начала координат.

б) Сжатие и расширение сигнала s₂ (t)=s₁ (nt) .

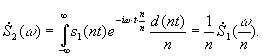
При сжатии сигнала в n раз на временной оси во столько же раз расширяется его спектр на оси частот при уменьшении модуля в n раз. Наоборот, при растяжении сигнала во времени имеет место сужение спектра и увеличение модуля спектральной плотности. Т. о. сжатие спектра импульса с целью повышения точности измерения частоты требует удлинения времени измерения. В то же время сжатие импульса по времени с целью, например, повышения точности измерения времени его появления заставляет расширять полосу пропускания измерительного устройства. В теории преобразования Фурье доказывается, что где

.

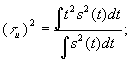
В реальности это проявление принципа неопределенности: При при несреднеквадратичном определении и .

в) Дифференцирование и интегрирование сигнала

Аналогично спектральная плотность интеграла равна

г) Сложение сигналов (линейность преобразования)

- из-за линейности операции интегрирования.

д) Спектр произведения двух функций

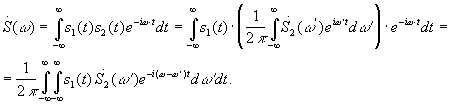
Изменяем порядок интегрирования:

Спектр произведения двух функций равен свертке их спектров (с множителем ).

Аналогично можно показать, что свертке двух функций 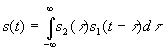соответствует спектр

являющийся произведением исходных спектров.

е) Взаимная обратимость s(t) и .

;

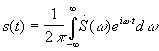Для четного сигнала s(t)=s(-t), и в связи с симметричностью пределов интегрирования в выражении для можно поменять знак в экспоненте Тогда, если по функциональной зависимости то

1.2 Распределение энергии в спектре непериодического сигнала

Найдем спектр квадрата функции s(t).

- используем свойства преобразования Фурье для произведения двух функций.

В частном случае ( ) будем иметь:

. Переходя от к и т. к. , комплексное сопряжение .

- равенство Парсеваля.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--