Экономико-математическое моделирование / Реферат: Сравнительный анализ динамики и выявление внутригодовых колебаний розничного товарооборота области

Реферат: Сравнительный анализ динамики и выявление внутригодовых колебаний розничного товарооборота области

Для этого можно использовать метод проверки разностей средних уровней. Суть этого метода состоит в делении ряда на две части и нахождении их средних и дисперсий по формулам:

где n – число уровней ряда;

;

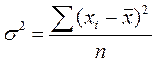Затем мы находим расчетное значение с помощью статистики Стьюдента:

;

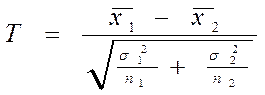Затем полученное значение сравниваем с критическим табличным значением , которое равно 3,18 (число степеней свободы равно n1 + n2 - 2).

Сравнив критическое значение с расчетным, делаем вывод о наличии или отсутствии тренда в рыду динамики.

В нашем случае Трасч. = 5,0528 и 4,2246 для первого и второго варианта соответственно. Т. к. в обоих случаях Тр. > Ткр., то гипотезу об отсутствии тренда отклоняем.

После ее исключения из колеблемости уровней временного ряда, рассчитаем уравнение тренда, воспользовавшись линейной функцией

где ;

;

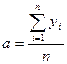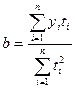С помощью полученного уравнения тренда выполним экстраполяцию на один год.

Найденные таким образом значения не учитывают сезонные колебания в объеме товарооборота. Для учета сезонной составляющей уровень, полученный в результате экстраполяции, умножают на индекс сезонности, т.е.

где - экстраполируемый уровень с учетом сезонных колебаний.

3.2 Корреляционная зависимость между уровнями различных рядов динамики.

Применение методов классической теории корреляции в динамических рядах связано с некоторыми особенностями. Прежде всего это наличие для большинства динамических рядов зависимости последующих уровней от предыдущих.

Наличие зависимости между последующими и предшествующими уровнями динамического ряда в статистической литературе называют автокорреляцией.

Коэффициент автокорреляции вычисляется по непосредственным данным рядов динамики, когда фактические уровни одного ряда рассматриваются как значения факторного признака, а уровни этого же ряда со сдвигом на один период принимаются в качестве результативного признака.

Коэффициент автокорреляции рассчитывается на основе формулы коэффициента корреляции для парной зависимости:

где y_t – фактические уровни ряда, а y_t ₊₁ – уровни того же ряда со сдвигом на 1 период.

4. Результаты работы программы.

Таблица 1 – Исходные данные (1 вариант).

Год	Янв.	Февр.	Март	Апр.	Май	Июнь	Июль	Авг.	Сент.	Окт.	Нояб.	Дек.	Итого
1-ый	92,4	77	50	36,6	67,5	53,3	70	74,8	80	85	95	106,4	888
2-ой	105	89	70	59	75	70	83	90	99	100	105	120	1065
3-ий	125	120	105	101	125	110	137	139	150	149	160	190	1611
4-ый	195	185	177	175	195	190	210	215	230	230	240	270	2512
5-ый	276	264	261	260	280	275	297	299	315	310	315	350	3502
Итого за весь период	793,4	735	663	631,6	742,5	698,3	797	817,8	874	874	915	1036,4	9578
Средний уровень за месяц	158,68	147	132,6	126,32	148,5	39,66	159,4	163,56	174,8	174,8	183	207,28	159,63333
Абсолютное отклонение от общей средней	-0,9533333	-12,633333	-27,033333	-33,313333	-11,133333	-19,973333	-0,2333333	3,9266667	15,166667	15,166667	23,366667	47,646667
Относительное отклонение от общей средней (в %)	-0,5972019	-7,9139695	-16,934642	-20,868657	-6,9743161	-12,512007	-0,1461683	2,4598037	9,5009397	9,5009397	14,637711	29,847567
Индекс сезонности	99,402798	92,08603	83,065358	79,131343	93,025684	87,487993	99,853832	102,4598	109,50094	109,50094	114,63771	129,84757

Таблица 2 – Исходные данные (2 вариант).

Год	Янв.	Февр.	Март	Апр.	Май	Июнь	Июль	Авг.	Сент.	Окт.	Нояб.	Дек.	Итого
1-ый	81,8	81	67,8	50,4	76,1	62	88	94,2	100	118	110,4	125	1054,999
2-ой	120	110	105	102	110	101	126	130	140	145	139	150	1478
3-ий	150	130	130	125	135	129	147	152	163	165	157	175	1758
4-ый	170	160	155	155	170	170	190	200	210	225	223	250	2278
5-ый	249	241	239	236	250	247	259	270	280	285	281	300	3137
Итого за весь период	770,8	722	696,8	668,4	741,1	709	810	846,2	893	938	910,4	1000	9705,7
Средний уровень за месяц	154,16	144,4	139,36	133,68	148,22	141,8	162	169,24	178,6	187,6	182,08	200	161,761
Абсолютное отклонение от общей средней	-7,602	-17,362	-22,402	-28,082	-13,542	-19,962	0,238	7,478	16,838	25,838	20,318	38,238
Относительное отклонение от общей средней (в %)	-4,699	-10,733	-13,849	-17,36	-8,371	-12,34	0,147	4,623	10,409	15,973	12,561	23,639
Индекс сезонности	95,301	89,267	86,151	82,64	91,629	87,66	100,147	104,623	110,409	115,973	112,561	123,639

Таблица 3 – Построение модели сезонной волны на основе гармоник ряда Фурье (1 вариант).

Удельный розничный товарооборот области по месяцам	y cos t	y sin t	yt	y cos 2t	y sin 2t	yt	y cos 3t	y sin 3t	yt	y cos 4t	y sin 4t	yt
158,68	158,68	0	166,242	158,68	0	170,618	158,68	0	157,127	158,68	0	152,293
147	127,306	73,5	152,273	73,5	127,306	146,902	-6,426	147	147,764	-73,5	127,306	148,646
132,6	66,3	114,835	140,277	-66,3	114,835	130,529	-132,6	-1,159	154,781	-66,3	-114,835	158,732
126,32	-5,522	126,32	133,468	-126,32	-1,104	129,091	1,654	-126,32	164,467	126,32	2,209	159,633
148,5	-74,25	128,605	133,669	-74,25	-128,605	139,041	148,5	2,596	159,014	-74,25	128,605	159,896
139,66	-120,949	69,83	140,828	69,83	-120,949	150,576	1,942	139,66	148,819	-69,83	-120,949	152,771
159,4	-159,4	-1,394	153,025	159,4	2,787	157,402	-159,4	-4,18	152,473	159,4	5,574	147,64
163,56	-141,647	-81,78	166,993	81,78	141,647	161,622	-8,448	-163,56	163,599	-81,78	141,647	164,481
174,8	-87,4	-151,381	178,989	-87,4	151,381	169,241	174,8	6,113	166,25	-87,4	-151,381	170,201
174,8	2,084	-174,8	185,799	-174,8	-4,169	181,422	-6,253	174,8	164,467	174,8	8,338	159,633
183	91,5	-158,483	185,598	-91,5	-158,483	190,969	-183	5,09	168,156	-91,5	158,483	169,038
207,28	179,51	-103,64	178,439	103,64	-179,51	188,187	0	-207,28	168,684	-103,64	-179,51	172,636
1915,6	39,649	-156,994	1915,6	26,26	-52,377	1915,6	6,98	-35,7	1915,6	-29	-10,635	1915,6

Таблица 4 – Построение модели сезонной волны на основе гармоник ряда Фурье (2 вариант).

Удельный розничный товарооборот области по месяцам	y cos t	y sin t	yt	y cos 2t	y sin 2t	yt	y cos 3t	y sin 3t	yt	y cos 4t	y sin 4t	yt
154,16	154,16	0	164,822	154,16	0	164,567	154,16	0	158,54	154,16	0	156,138
144,4	125,054	72,2	151,183	72,2	125,054	145,993	-6,312	144,4	150,948	-72,2	125,054	150,172
139,36	69,68	120,689	140,379	-69,68	120,689	135,444	-139,36	-1,218	156,987	-69,68	-120,689	160,165
133,68	-5,843	133,68	135,304	-133,68	-1,169	135,559	1,753	-133,68	164,163	133,68	2,337	161,762
148,22	-74,11	128,362	137,319	-74,11	-128,362	142,509	148,22	2,592	160,532	-74,11	128,362	159,755
141,8	-122,802	70,9	145,883	70,9	-122,802	150,818	1,972	141,8	155,613	-70,9	-122,802	158,792
162	-162	-1,416	158,702	162	2,832	158,447	-162	-4,249	160,18	162	5,665	157,778
169,24	-146,566	-84,62	172,34	84,62	146,566	167,15	-8,74	-169,24	166,218	-84,62	146,566	165,442
178,6	-89,3	-154,672	183,145	-89,3	154,672	178,21	178,6	6,245	164,983	-89,3	-154,672	168,161
187,6	2,237	-187,6	188,219	-187,6	-4,474	188,474	-6,711	187,6	164,163	187,6	8,948	161,762
182,08	91,04	-157,686	186,205	-91,04	-157,686	191,395	-182,08	5,06	169,348	-91,04	157,686	168,571
200	173,205	-100	177,641	100	-173,205	182,576	0	-200	169,463	-100	-173,205	172,642
1941,14	18,361	-158,746	1941,14	-1,53	-35,074	1941,14	-2,46	-29,12	1941,14	-14,41	-13,7	1941,14

Таблица 5 – Выявление типов колебаний внутригодичной динамики уровней временного ряда (1 вариант).

Год	Квартал	Фактический объем товарооборота	Скользящая средняя за 4 квартала	Центрированная скользящая средняя за 4 квартала	Отношение фактического объема товарооборота к скользящей средней	Индекс сезонности	Объем товарооборота, скорректированный на индекс сезонности
1	1	73,133				1,036	70,606
	2	52,467	74			0,913	57,451
	3	74,933	77,717	75,858	0,988	0,995	75,297
	4	95,467	81,6	79,658	1,198	1,056	90,422
2	1	88	85,533	83,567	1,053	1,036	84,959
	2	68	88,75	87,142	0,78	0,913	74,46
	3	« 1 2 3 » К-во Просмотров: 298 Бесплатно скачать Реферат: Сравнительный анализ динамики и выявление внутригодовых колебаний розничного товарооборота области >>> Скачать <<< Меню Сочинения Биографии Краткие содержания Анализ Критика Характеристики Как писать слова Рефераты Вопросы Поиск