Реферат: Статистическая устойчивость случайных событий

2.Подсчитать число появлений m_і события А в каждой серии.

3.Вычислить частоту ω_i (A) появления событий А в каждой серии/

4.Объединив результаты опытов 1 и 2, затем 1, 2, 3 и т.д. до последней серии опытов в задании, вычислить:

N_і – число опытов в объединённых (накопленных) сериях испытаний.

M_і – число появления события А в объединенных (накопленных) сериях

испытаний.

W_і (А) – частоту появления события А в объединенных (накопленных) сериях испытаний.

5. Результаты вычислений занести в таблицу 1.

6. Построить точечную диаграмму №1. Зависимость ω_i (A) от номера серииі=1, 2, ... k.

7.Построить точечную диаграмму №2. Зависимость W_k (А)от числа опытов в серии N_і .

8. Сравнить полученные диаграммы и сделать вывод о статической устойчивости события А.

9. Вычислить или найти в приложении 1 и 2 вероятность появления события А Р(А).

10. Вычислить вероятность противоположного события, пользуясь формулой q = 1 -p.

11.Найти отклонение относительной частоты Wk(А) от его статистической вероятности Р(А), пользуясь формулой e=÷W_k (А)-Р(А)÷.

12.Изобразить на точечной диаграмме №2 линии, соответствующие значениям Р(А),Р(А)+e и Р(А)-e.

13. Вычислить вероятность того, что отклонение относительной частоты от постоянной вероятности р по абсолютной величине не превышает заданного числа e>0.

14. Определить, находится ли в пределах заданной величины e отклонение частоты W_k (А) от его статистической вероятности Р(А).

15.Оценить минимальное число опытов, необходимых для стабильного получения отклонений частоты W_k (А) от его статистической вероятности Р(А)в пределах заданной величины e, для доверительной вероятности γ = 0,95 по формуле

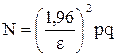
16.Сделать выводы.

Замечания

1.Все вычисления производить с точностью до 0,001.

2.Точечные диаграммы строить на миллиметровой бумаге, выбирая масштаб в зависимости от полученных числовых значений величины W_і (А).

Контрольные вопросы.

1. Какие события называются случайными?

2. Что называется частотой случайного события А?

3. Какое событие называется статистически устойчивым?

4. Сформулировать статистическое определение вероятности.

5. Сформулировать классическое определение вероятности.

6. Как определить вероятность отклонения частоты W(A) случайного события А от его вероятности Р(А) в независимых испытаниях?

7. Какая функция называется функцией Лапласа? Сформулировать свойства функции Лапласа.

8. Как найти вероятность события противоположного событию А?