Реферат: Статистические оценки критериев надежности РЭСИ
λ /r1
m>1
λ /r4
m=1
λ /r3
Значения оценки λ определяется по соответствующей строке таблицы 4, коэффициенты r 1 , r2 , r3 , r4 , r5 , r0 определяются по соответствующим графам таблиц по доверительной вероятности γ, значениям m и n.
Доверительные границы для α плана [ NUT ] находят из п.3 таблицы 4, при этом:
![]() (1)
(1)
![]() , (2)
, (2)
где
![]() ; (3)
; (3)
![]()
![]() . (4)
. (4)
![]() ; (5)
; (5)
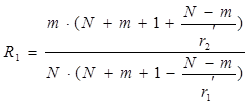 ; (6)
; (6)
![]() . (7)
. (7)
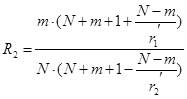 ; (8)
; (8)
Коэффициенты r 1 и r2 находят по таблице в зависимости от значения j и m .
Коэффициенты r1 ' и r2 ' находят по этим же таблицам, в которые входят по значениям j и m '= N - m .
Доверительные границы для λ H и λ B в случае плана [ N , U , T ] находят с помощью уравнений предыдущего пункта при:
![]() (9)
(9)![]()
Распределение Пуассона
Распределение Пуассона имеет один параметр а , который равен математическому ожиданию случайной величины. Оценка данного параметра дается формулой:
α=К , (10)
где К - наблюдаемое значение случайной величины. Соответственно:
α H =К/ r 1 и αв =К/г3 , если К≠0 . (11)
Если К=0, α H =0, α B = r 0 , то соответственно r0 , r1 ,r2 находят по соответствующим таблицам по значению j и m=К .
Если из партии изделий объема N берется выборка объема n , то случайное число К дефектных изделий в выборке имеет Пуассоновское распределение при выполнении 2-х условий:
n<0,1N ,
доля q дефектных изделий в партии не превосходит 0,1.
При выполнении этих условий а = n ∙ q