Реферат: Стационарные одномерные движения одной частицы 2

3.2.3. Частные решения выберем в виде комплексных экспонент

, (3.29)

По физическим соображениям можно волновой функции придать вид лишь одного из частных решений. Это связано со свойствами момента импульса в стационарном вращательном движении, которые мы рассмотрим в рамках соответствующего операторного уравнения

, т.е.

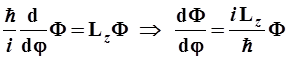, (3.30)

откуда следует, что собственная волновая функция оператора имеет вид:

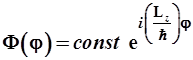. (3.31)

Функции (3.29) и (3.31) совпадают при условии, что

или

Физический смысл знака проекции L_z связан с ориентацией вектора вдоль или против оси вращения, а это, в свою очередь, зависит от направления вращения плоского ротатора.

Таким образом, в качестве волновых функций удобны частные решения уравнения Шредингера вида (3.29), имеющие ясный физический смысл функций состояния с определенной ориентацией вращения. Далее займемся доводкой полученных решений до волновых функций вращательных состояний. Эти решения заведомо удовлетворяют свойствам конечности и неразрывности, но пока не обладают свойством однозначности, а также нуждаются и в нормировке. Нормировочный коэффициент А легко получается из равенств:

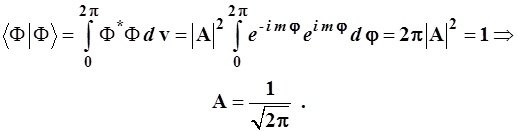(3.32)

3.2.4. Обратимcя к выяснению природы параметра m на основе свойства однозначности, которое состоит в том, что значение волновой функции Φ отвечающей аргументу φ , совпадает со значением функции, аргумент которой сдвинут на полный оборот и равен , т.е.:

. (3.33)

Число последующих поворотов неограничено, и поэтому вполне достаточно условия (3.33). Это означает:

,

откуда следует, что , т.е. получим систему уравнений

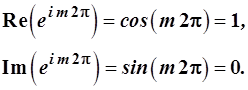(3.34)

Требования (3.34) выполняются только при целочисленных значениях параметра m , пробегающих с интервалом 1 все значения, включая 0:

, (3.35)

и комплексные нормированные волновые функции плоского ротатора приобре-тают вид: 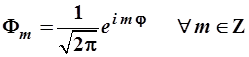. (3.36)

3.2.5. В результате оказывается, что энергия вращения квантована, и уровни, определяемые формулой (3.30) можно пронумеровать, т.е.:

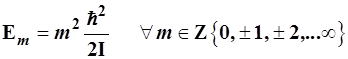. (3.37)

Состояния, отличающиеся только знаком m , т.е. направлением вращения, обладают равной энергией. За исключением нулевого уровня () всем прочим уровням отвечает по два состояния, это означает, что каждый из уровней дважды вырожден . Вырождение вращательных уровней плоского ротатора является следствием; равноправия двух направлений вращения вокруг оси. Принимая за единицу шкалы энергии

3.2.6. Обсудим волновые функции, для чего воспользуемся приемом, который имеет далеко идущие последствия. Он связан с переходом от комплексной формы волновых функций, компактной, но не обладающей графической наглядностью, которая чрезвычайно важна и желательна для химических приложений, к функциям вещественного вида. Это достигается на основе принципа суперпозиции путем составления линейных комбинаций комплексных экспонент с одинаковым значением модуля , т.е. вместо волновых функций вида при будем использовать функции вида

. (3.38)

Согласно теореме об общих решениях дифференциальных уравнений, такой переход допустим, и линейные комбинации описывают состояния, которые принадлежат тем же самым уровням энергии, но при этом теряется определенность в ориентации вращения относительно выбранной оси. Так часто случается в квантовой механике: добиваясь наглядности в описании какого-либо свойства, неизбежно теряют в других.