Реферат: Степенные ряды
формула Даламбера:
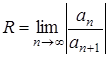 ;(1.3)
;(1.3)
формула Коши:
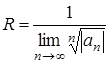 .(1.4)
.(1.4)
Если в формуле Коши ![]() , то полагают
, то полагают ![]() , если
, если ![]() , то полагают
, то полагают ![]() .
.
Пример 1.1. Найти радиус сходимости, интервал сходимости и область сходимости степенного ряда  .
.
Решение
Найдем радиус сходимости данного ряда по формуле

В нашем случае
 ,
,  .
.
Тогда  .
.
Следовательно, интервал сходимости данного ряда имеет вид  .
.
Исследуем сходимость ряда на концах интервала сходимости.
При ![]() степенной ряд превращается в числовой ряд
степенной ряд превращается в числовой ряд
 .
.
который расходится как гармонический ряд.
При ![]() степенной ряд превращается в числовой ряд
степенной ряд превращается в числовой ряд
 .
.
Это – знакочередующийся ряд, члены которого убывают по абсолютной величине и ![]() . Следовательно, по признаку Лейбница этот числовой ряд сходится.
. Следовательно, по признаку Лейбница этот числовой ряд сходится.
Таким образом, промежуток  – область сходимости данного степенного ряда.
– область сходимости данного степенного ряда.
2. Свойства степенных рядов
Степенной ряд (1.2) представляет собой функцию ![]() , определенную в интервале сходимости
, определенную в интервале сходимости ![]() , т. е.
, т. е.
![]() .
.
Приведем несколько свойств функции ![]() .
.
Свойство 1. Функция ![]() является непрерывной на любом отрезке
является непрерывной на любом отрезке ![]() , принадлежащем интервалу сходимости
, принадлежащем интервалу сходимости ![]() .
.
Свойство 2. Функция ![]() дифференцируема на интервале
дифференцируема на интервале ![]() , и ее производная
, и ее производная ![]() может быть найдена почленным дифференцированием ряда (1.2), т. е.
может быть найдена почленным дифференцированием ряда (1.2), т. е.