Реферат: Связанные контуры с ёмкостной и индуктивной связью
Рис. 1
Вывод : В радиоприемных устройствах наиболее широко применяются схемы с внешнеемкостной связью, когда оба контура имеют одинаковые параметры. Проанализируем частотные свойства таких связанных контуров.
ОБЩЕЕ ВЫРАЖЕНИЕ АЧХ СВЯЗАННЫХ КОНТУРОВ С ИНДУКТИВНОЙ СВЯЗЬЮ
Схема системы связанных контуров при индуктивной связи между ними изображена на рис. 2.

Рис. 2
Поставим задачу – найти КПФ (![]() ) указанной системы, определив ее в виде отношения комплексного тока во втором контуре к комплексной ЭДС генератора. Для этой цепи составим уравнения для контурных токов:
) указанной системы, определив ее в виде отношения комплексного тока во втором контуре к комплексной ЭДС генератора. Для этой цепи составим уравнения для контурных токов:
 ,
,
 .
.
Из 2-го уравнения определим ![]() и подставим в 1-е уравнение:
и подставим в 1-е уравнение:
 ,
,
 .
.
Отсюда:
 .
.
Для выражения, заключенного в квадратные скобки, произведем преобразования, которые выполнялись для одиночного колебательного контура. Тогда:
 ,
,
где ![]() – добротность контура;
– добротность контура;
![]() – резонансная частота контура;
– резонансная частота контура;
 – относительная расстройка контура;
– относительная расстройка контура;
![]() – обобщенная расстройка контура.
– обобщенная расстройка контура.
Если частотную характеристику рассматривать в относительно узкой полосе частот (вблизи резонансной), то можно пренебречь частотной зависимостью ![]() и считать:
и считать: ![]() .
.
Тогда
 .
.
Обозначим ![]() – параметр связи (фактор связи) причем
– параметр связи (фактор связи) причем ![]() , т.е. зависит от добротности, где
, т.е. зависит от добротности, где ![]() – коэффициент связи.
– коэффициент связи.
Окончательное выражение КПФ связанных контуров имеет вид:
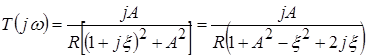 .
.
Взяв модуль от КПФ, получим выражение для АЧХ:
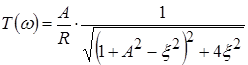 .
.
Вывод : Это общее выражение для АЧХ содержит фактор связи ![]() и переменную величину
и переменную величину ![]() – обобщённую расстройку . Оно будет удобным для исследования частотных характеристик связанных контуров.
– обобщённую расстройку . Оно будет удобным для исследования частотных характеристик связанных контуров.