Реферат: Свойства усредненной функции с сильной осцилляцией
Это название оправдано так как из (1) и теоремы о среднем для интегралов можем заключить
![]()
![]()
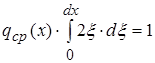
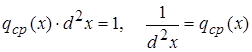
§ 2 Свойства функции ![]() .
.
1. Если ![]() , при
, при ![]() , то
, то ![]() при
при ![]()
Доказательство:
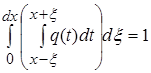 ,
, ![]() ,
, ![]()
![]() " N >0,
" N >0, ![]() :
: ![]()
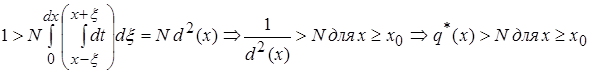
2. 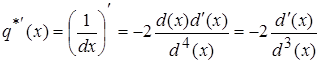 (2)
(2)
3. 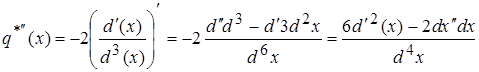 (3)
(3)
Дифференцируя формулу (1) по dx получаем
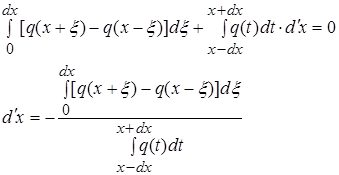 (4)
(4)
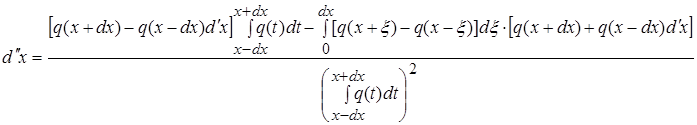 (5)
(5)
§ 2 Свойства функции ![]() и ее производных.
и ее производных.
I) Рассмотрим вид функции 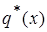 для случаев когда
для случаев когда 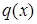 :
:
2.1 ![]()
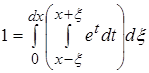
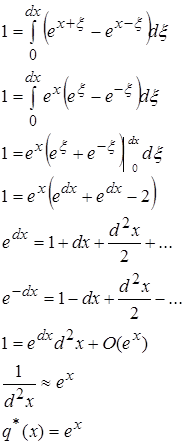
2. 2 ![]()
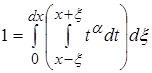
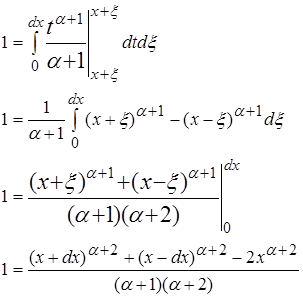
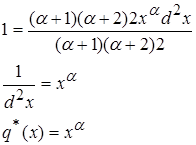
2 .3 ![]() где a>0;
где a>0;
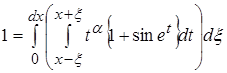
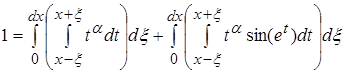
Разделим интеграл на два интеграла и вычислим их отдельно.
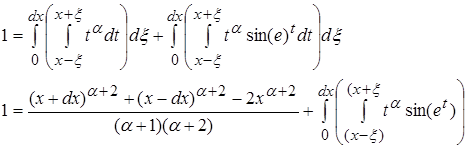
Второй интеграл не оказывает влияния на первый, так как при ![]() функция стремится к 0.
функция стремится к 0.
Доказательство:
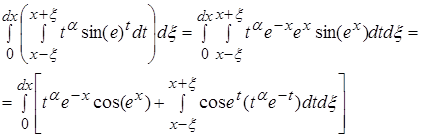
Рассматривая второй интеграл, мы получаем:
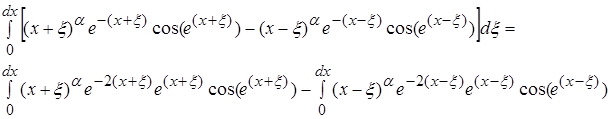
Рассматривая первый интеграл, получаем:
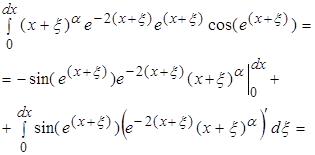
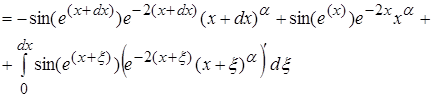
Последние два слагаемых полученных при интегрировании содержат в произведении ![]() , то есть при возрастании x эти слагаемые будут очень быстро уменьшатся и весь интеграл при
, то есть при возрастании x эти слагаемые будут очень быстро уменьшатся и весь интеграл при ![]() становится очень малым по сравнению с первой частью. Поэтому можно считать что при
становится очень малым по сравнению с первой частью. Поэтому можно считать что при ![]()
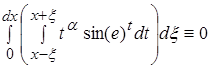
Следовательно:
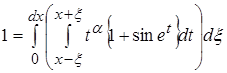
![]()
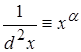
2.4. ![]()

Наложить на![]() ограничение, такое чтобы
ограничение, такое чтобы ![]() присутствие
присутствие ![]() не влияло на поведение функции.
не влияло на поведение функции.


Рассматривая полученное выражение можно заметить что

становится пренебрежительно малым по отношению к остальной части
как только ![]() . Ограничение №1
. Ограничение №1
В тоже время

Становится бесконечно малым как только ![]() . Ограничение №2
. Ограничение №2
Раскрывая в оставшейся части скобки, по Биному Ньютона получаем, что
![]()
должен быть очень малым при ![]() то есть
то есть
![]()
так как ![]() ограниченная функция, к 0 должен стремится
ограниченная функция, к 0 должен стремится ![]() .
.
![]()
![]()
![]()
![]() Ограничение №3
Ограничение №3
Учитывая ограничения 1, 2, 3 получаем:
![]()
Следовательно, ![]() ограничение на
ограничение на ![]() удовлетворяющее поставленной задаче, при котором присутствие
удовлетворяющее поставленной задаче, при котором присутствие ![]() не влияет на поведение функции
не влияет на поведение функции ![]() .
.
§ 3 Рассмотрим поведение функции ![]() для случаев:
для случаев:
3.1) ![]()

![]()
![]()