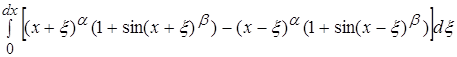Реферат: Свойства усредненной функции с сильной осцилляцией

3.3)

Вычислим отдельно интегральное выражение, стоящее в числителе:

=

=

рассматривая пределы при видим что на поведение функции оказывает влияние только главный член

Поведение данной функции при эквивалентно поведению функции

(*)

Вычислим интеграл в знаменателе:

=

(**)

Учитывая (*)и (**) получаем

Следовательно, по формуле (2) получаем

3.4

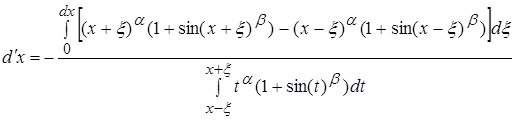
Отдельно вычислим числитель и знаменатель:

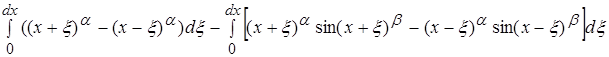
По ранее доказанному в пункте 2.4 мы можем сказать что второй интеграл не оказывает влияния на поведение функции. Поэтому мы можем утверждать, что числитель эквивалентен выражению:

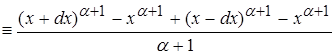
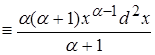
Вычислим знаменатель:

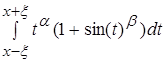
Разделив интеграл на 2 интеграла, мы получаем:

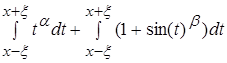
По пункту 2.4 можем вывести что второй интеграл не влияет на поведение функции при

Следовательно, знаменатель:

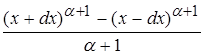
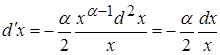
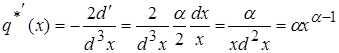
§4. Рассмотрим поведение второй производной

Для облегчения вычислений введем обозначения:

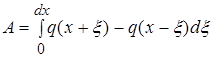
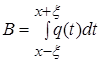
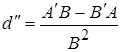При этом формула для примет вид (6)

4.1
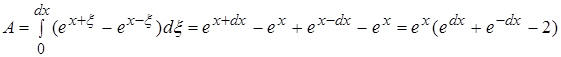
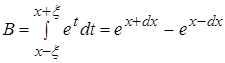