Реферат: Сжатие речевого сигнала на основе линейного предсказания

2. ошибка была минимальна.

Для получения передаточной функции ФФ, наиболее точно воспроизводящего частотную характеристику голосового тракта для данного звука, следует определять коэффициенты передаточной функции исходя из условия наименьшей ошибки линейного предсказания речевого сигнала (по условию минимума среднего квадрата ошибки).

Запишем выражение для оценки дисперсии сигнала ошибки, которую надо свести к минимуму:

; ;

Получили, что - функция нескольких переменных. Продифференцируем ее и приравняем частные производные для нахождения экстремума:

; ,

где - символ Кронекера. Следовательно: ;

; => ;

Получили нормальные уравнения или уравнения Юла-Волкера. Введем обозначение: , где - есть ни что иное, как корреляционная функция. Перепишем полученное выражение с учетом принятого обозначения:

(*)

Для вычисления функции необходимо определить пределы суммирования по n : , где N – количество отсчетов в сегменте РС, а M - количество отсчетов, необходимых для расчета коэффициентов предсказания (M + 1)-го отсчета. Значит, первое предсказанное значение запишется так: , где n = M + 1.

Получили:

;

Обозначим n – k = j => n = k + j , n – m = k + j – m <=> n – m = i + j , где i = k – m . Следовательно:

Таким образом, получается выражение, имеющее структуру кратковременной ненормированной АКФ, но зависящей не только от относительного сдвига последовательности i , но и от положения этих последовательностей внутри сегмента РС, которые определяются индексом k , входящим в пределы суммирования. Такой метод определения функции называется ковариационным .

Выражение (*) представляет собой систему линейных алгебраических уравнений (СЛАУ) относительно , у которых все коэффициенты различны.

При использовании ковариационного метода получаются несмещенные оценки коэффициентов линейного предсказания, то есть E{a_k }= a_{k .ист} , где a_{k .ист} – истинные значения коэффициентов линейного предсказания.

Другой способ определения коэффициентов системы (*) состоит в том, что вместо функции используется некоторая другая функция , которая определяется как

,

где - ненормированная кратковременная АКФ. Поскольку определение функции сводится к расчету АКФ, то такой метод называется автокорреляционным. При использовании этого метода мы получаем смещенные оценки коэффициентов линейного предсказания (однако, при M << N смещение пренебрежимо мало).

Перепишем СЛАУ (*) с учетом введенной функции :

.

.

При использовании автокорреляционного метода вся информация о сигнале, необходимая для определения коэффициентов линейного предсказания, содержится в кратковременной ненормированной АКФ B (i ).

Распишем полученную систему линейных алгебраических уравнений (СЛАУ) в явном виде:

Перепишем ее в матричной форме:

;

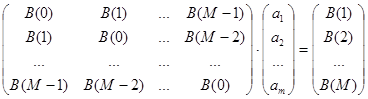Свойства матрицы коэффициентов системы:

1) матрица симметрична;

2) матрица Теплица (матрица, в пределах каждой диагонали которой все элементы равны);

Для решения СЛАУ с такой матрицей используется алгоритм Левинсона – Дурбина, который требует меньших вычислительных затрат, чем стандартные алгоритмы. Он выглядит следующим образом.

Начальные значения для алгоритма:

Алгоритм:

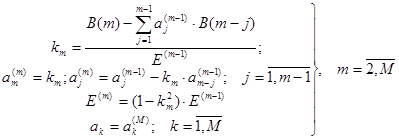
Решетчатый фильтр сигнала ошибки предсказания

В предыдущем разделе приводилась процедура вычисления коэффициентов предсказания Левинсона-Дурбина. В этой процедуре, как промежуточные величины, используются некоторые коэффициенты k_m , которые называются коэффициентами отражения. Их физический смысл заключается в следующем. Голосовой тракт человека представляет собой трубу, состоящую из секций, соединенных последовательно, но имеющих разный диаметр. При прохождении звуковой волны через такую систему, возникают отражения на стыках секций, т.к. каждый стык является неоднородностью. Коэффициент отражения характеризует величину проходимости стыка двух секций (сред). Коэффициент отражения равен:

.

Поясним его смысл на следующем рисунке («жирным» показана m – секция голосового тракта):

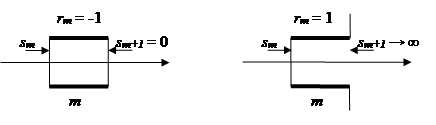
Если r_m = -1, то произойдет обрыв в цепи передачи сигнала (обрыв прямой ветви). Такого быть не должно, поэтому необходимо следить за этим.