Реферат: Технико-экономическое обоснование выбора проектного решения

– широкий диапазон регулирования подачи;

– плавность регулирования подачи;

– точность и стабильность базирования;

– точность обработки;

– качество обработки;

– устойчивость к вибрациям;

– высокая износостойкость;

– защищенность от перегрузок;

– низкий уровень шума;

– отсутствие монотонности в работе оператора;

– легкость обслуживания;

– простота системы управления;

– отсутствие "капризных" механизмов, требующих частой наладки;

– простота и удобство наладки станка.

Для каждого конкретного случая проектирования технической системы конструктор подбирает перечень критериев развития из списка глобальных и частных критериев. Основой для выбора служат требования, предъявляемые к проектируемой системе. При этом уже на стадии выбора проектного решения конструктор стремится, чтобы система максимально удовлетворяла всем выбранным критериям.

Контрольные вопросы и задания

1. Как называют параметры технического объекта, зависимые и независимые от окружающей среды?

2. Что такое критерии развития?

3. Приведите классификацию критериев развития.

4. Как критерии развития учитывают преемственность технических объектов?

5. Поясните сущность критерия расчленения технического объекта на элементы.

6. Что учитывают эргономические критерии развития?

7. Какие критерии называют общими и частными?

19.3. Оптимизация технических решений

19.3.1. Общие сведения

Для решения задачи оптимизации необходимо иметь множество возможных (альтернативных) решений Y (рис. 35). В этом множестве можно выделить множество допустимых решений Y _д . Решение называют допустимым, если оно удовлетворяет ограничениям (требованиям, предъявляемым к объекту): ресурсным, социальным и т.д. При этом

Y _д Í Y ,

где символ Í означает, что множество Y_д есть часть или совпадает с множеством Y возможных решений. В множестве допустимых решений можно выделить множество эффективных решений Y_э , которое включает в себя несравнимые между собой наилучшие решения:

Y_э Í Y_д .

Решение Y_э называется оптимальным, если оно обеспечивает экстремум (максимум, минимум) одновременно всех критериев. Оптимальное решение находится в множестве эффективных решений:

Y_о Í Y_э .

Поскольку все критерии одновременно не могут принять экстремальные значения, то при решении многокритериальной задачи находят только рациональное решение.

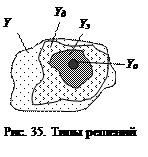Таким образом, задача оптимизации направлена на определение наилучшего (рационального) решения, путем последовательного сужения множеств Y , Y_д , Y _э в соответствии с допустимыми ограничениями и принятыми критериями [45, 46]:

Y _о Í Y _э Í Y _д Í Y .

Чем больше подобрано альтернативных вариантов, и чем более удачно подобраны критерии, тем больше вероятность того, что найденное решение будет самым лучшим.

В инженерной практике оптимизации можно отметить два правила: