Реферат: Теорема Штольца
которая представляет неопределённость вида ![]() .
.
Полагая в теореме Штольца
xn =1k +2k +…+nk , yn =nk+1 ,
будем иметь
![]() .
.
Но
(n-1)k+1 =nk+1 -(k+1)nk +… ,
так что
nk+1 -(n-1)k+1 =(k+1)nk +…
и
![]() .
.
5. Определим предел варианты
![]() ,
,
представляющей в первой форме неопределенность вида ![]() , а во второй – вида
, а во второй – вида ![]() . Произведя вычитание дробей, получим на этот раз неопределенное выражение вида
. Произведя вычитание дробей, получим на этот раз неопределенное выражение вида ![]() :
:
![]() .
.
Полагая xn равным числителю этой дроби, а yn – знаменателю, применим еще раз ту же теорему. Получим
![]() .
.
Но ![]() ,
,
а ![]() ,
,
так что, окончательно,
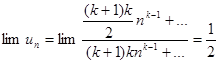 .
.
Пример 1.
![]() =
=![]() =
=![]() =
=![]() =
=![]() =
=![]() =
= ![]() =
=![]()
![]() =
=![]() =
=![]() .
.
Пример 2.
![]() =
=
=![]() =
=
=![]() =
=
=![]() =
=
=![]() =
=
=![]() =
=
=![]() .
.
Пример 3.
![]()
=![]()
=![]() .
.
Теорема Штольца справедлива для последовательностей, но т.к. последовательности есть частный случай функций, то эту теорему можно обобщить для функций.
Теорема.
Пусть функция ![]() , причем, начиная с некоторой xk , g(xk +1)>g(xk ), т.е. функция возрастающая.
, причем, начиная с некоторой xk , g(xk +1)>g(xk ), т.е. функция возрастающая.
Тогда![]() ,
,
если только существует предел справа конечный или бесконечный.
Доказательство:
Допустим, что этот предел равен конечному числу k
![]() .
.
Тогда, по определению предела ![]()

или
![]() .
.
Значит, какой бы ![]() ни взять, все дроби
ни взять, все дроби
![]() ,
, ![]() , …,
, …, ![]()
лежат между этими границами. Так как знаменатели их, ввиду возрастания g(xn ) вместе с x(n), положительны, то между теми же границами содержится и дробь ![]() , числитель которой есть сумма всех числителей, написанных выше дробей, а знаменатель – сумма всех знаменателей. Итак, при
, числитель которой есть сумма всех числителей, написанных выше дробей, а знаменатель – сумма всех знаменателей. Итак, при ![]()
 .
.
Напишем тождество(которое легко проверить):
 ,
,