Реферат: Теории электрической связи: Расчет приемника, оптимальная фильтрация, эффективное кодирование

При частотной модуляции сигналы S₁ (t) и S₂ (t) являются взаимоортогональными, в связи с этим функция взаимной корреляции равна нулю. И так как амплитуды сигналов S₁ (t) и S₂ (t) равны, то Е₁ =Е₂ . В результате чего Е_э =2Е₁ , а аргумент функции Крампа будет равен: h₀ .

Поэтому подставляя эту величину в формулу вероятности получим: - вероятность ошибки, при ДЧМ. (5)

S₁

ДЧМ рис. 6

0 S₂

На рис.6 представлена векторная диаграмма ДЧМ, на которой можно заметить, что расстояние между векторами (взаимоортогональные сигналы) равно . Заметим, что по сравнению с ДАМ, мы получаем двойной выигрыш по мощности.

ДИСКРЕТНАЯ ФАЗОВАЯ МОДУЛЯЦИЯ (ДФМ).

При ДФМ сигнал, поступающий на вход приемника имеет следующий вид:

В данном случае аргумент функции Крампа будет равен:

Поэтому подставляя эту величину в формулу вероятности ошибки получим:

(6)

S₁

ДФМ 0 рис.7

S₂

Из приведенной векторной диаграммы видно, что расстояние между векторами сигналов равно 2S₁ . Энергия пропорциональна квадрату разности сигналов.

Заметим, что по сравнению с ДАМ мы получим четырехкратный выигрыш по мощности.

Следует уточнить, что приведенные данные о энергии сигналов ДАМ, ДЧМ и ДФМ относятся к пиковым мощностям этих сигналов. В этом смысле при переходе от ДЧМ к ДАМ мы имеем двукратный выигрыш в пиковой мощности, однако при ДАМ сигналы имеют пассивную паузу, т.е. мощность сигналов в паузе равна нулю, поэтому по потребляемой передатчиком мощности, кроме проигрыша по мощности, имеется еще и двукратный выигрыш. С учетом этого, при переходе от ДЧМ к ДАМ проигрыш по мощности компенсируется двукратным выигрышем за счет пассивной паузы ДАМ, в результате чего по потребляемой мощности эти сигналы оказываются равноценными, однако при ДАМ трудно установить необходимый порог в сравнивающем устройстве, а при приеме сигналов ДЧМ регулировка порога не требуется, в связи с этим свойством ДЧМ применяется чаще, чем ЧАМ.

Вероятность ошибки зависит от вероятности некорректного приема сигналов S₁ и S₂ , но при применении приемника Котельникова предполагается что канал связи – симметричный, т.е. совместные вероятности передачи и приема сигналов

S₁ и S₂ равны. Исходя из этого запишем формулу вероятности ошибки: 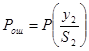(7)

Возьмем формулу 7 за основу для определении вероятности ошибки в приемнике Котельникова.

Предположим, что нам известно, что на вход приемника поступает сигнал S₁ (t) . в этом случае используя правило приемника Котельникова, в котором должно выполняться следующее неравенство:

(8)

При сильной помехе знак неравенства может измениться на противоположный, в результате чего вместо сигнала S₁ (t) на вход может поступить сигнал S₂ (t), т.е. произойдет ошибка. Поэтому вероятность ошибки можно рассматривать, как вероятность изменения знака неравенства (8). Подставляя вместо x(t)=S₁ (t)+n(t) . Преобразовывая получаем:

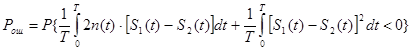(8)

Вероятность ошибки в приемнике Котельникова, выраженная, через эквивалентную энергию Е_э , которая представляет собой разность сигналов S₁ (t) и S₂ (t) и будет определяться формулой:

Формулы вероятности ошибки для ДАМ, ДЧМ и ДФМ. Приведены соответственно: 6, 5, 4.

2.1.2. Преобразование приемника Котельникова применительно к фазовой модуляции.

Приемник Котельникова, являющийся идеальным и обеспечивающий оптимальную помехоустойчивость использует для приема и распознавания информации, передаваемой по каналу связи все параметры передаваемого сигнала (фаза, частота, амплитуда), кроме того в приемнике Котельникова, в отличии от реального приемника отсутствуют фильтры на входе, обеспечивающие фильтрацию помех. Схема приемника Котельникова приведена на рис. . В качестве опорного генератора применим фазовый опорный гетеродин. Схема преобразованного приемника приведена на рис.8.