Реферат: Теории электрической связи: Расчет приемника, оптимальная фильтрация, эффективное кодирование

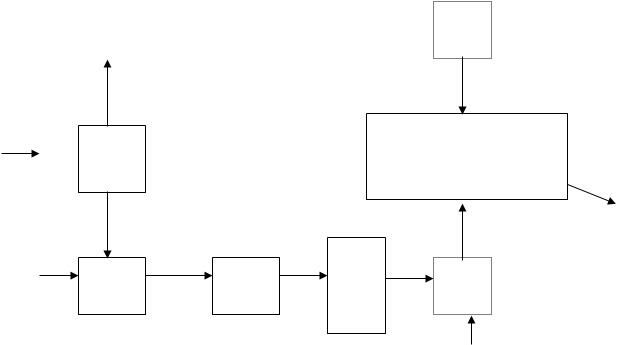
Рис.8

Вычислим отношение энергии сигнала Е к спектральной плотности N₀ .

Энергия сигнала при фазовой модуляции вычисляется по формуле:

E_э =Pc T (2.1.)

, откуда отношение энергии к спектральной плотности сигнала будет равно:

;

Найдем вероятность ошибки в приемнике Котельникова, применительно к фазовой модуляции.

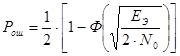; (2.2.) ; .

Из сравнения потенциальной помехоустойчивости приемника Котельникова с потенциальной помехоустойчивостью когерентного приемника с фазовой модуляцией, можно сделать вывод, что помехоустойчивость приемника, использующего в качестве информационного параметра фазу, почти приближена к вероятности ошибки приемника Котельникова.

3. Оптимальная фильтрация.

Отметим, что оптимальный приемник, является корреляционным, сигнал на его выходе представляет собой функцию корреляции принимаемого и ожидаемого сигналов, благодаря чему обеспечивается максимально-возможное отношение сигнал/шум.

Так как определение функции корреляции является линейной, то её можно реализовать в некотором линейном фильтре, характеристики которого являются такими, что отношение сигнал/шум на его выходе получается максимальным. Задача оптимальной фильтрации непрерывного сигнала ставится так, чтобы обработав принятый сигнал, получить на выходе приемника сигнал, наименее отличающийся от переданного сигнала. Решение этой задачи основывается на трех основных предположениях:

1. Сигнал S(t) и помеха w(t) представляют собой стационарные случайные процессы;

2. Операция фильтрации предполагается линейной;

3. Критерием оптимальности считается минимум среднеквадратичной ошибки.

Рассмотрим задачу синтеза фильтров, которые используются в схемах обнаружения и различения дискретных сигналов. Как правило эти фильтры ставятся перед решающим устройством, задача которого – вынести решение в пользу того или иного сигнала. Нужно отметить важное обстоятельство, что при приеме дискретных сигналов нет необходимости заботиться о сохранении формы сигнала. Основная задача – обеспечить минимум ошибочных решений при приеме сигналов. Очевидно, что вероятность ошибочного приема будет уменьшаться. Поэтому при синтезе фильтров для дискретных сигналов используется критерий максимума отношения сигнал/шум на выходе фильтра. Фильтры, удовлетворяющие данному критерию могут называться оптимальными фильтрами , или фильтрами, максимизирующими отношение сигнал/шум.

На вход фильтра с передаточной функцией K(jw) подается смесь сигнала S(t) и помехи n(t). Полагаем сигнал полностью известным, неизвестным считается лишь факт его присутствия. Известны также статистические характеристики шума (помехи). Требуется синтезировать такой фильтр (т.е. К_опт (jw)), который обеспечивал бы на выходе в заданный момент времени (момент принятия решения) t₀ наибольшее отношение пикового значения сигнала y(t₀ ) к среднеквадратичному шуму s_n :

(3.1.)

Рассмотрим случай, когда шум на входе фильтра имеет равномерный энергетический спектр G(w)=n₀ ² (белый шум). Сигнал может быть задан своей временной функцией S(t) или комплексным спектром.

комплексный коэффициент передачи фильтра представим в форме:

тогда для сигнала и дисперсии шума на выходе фильтра можно записать:

(3.2.)

(3.3.)

Примем t₀ – как некоторый фиксированный момент времени, при котором амплитуда на выходе фильтра достигает своего максимального значения. Для этого значения времени получим:

(3.4.)

отношение квадрата пикового значения сигнала к дисперсии шума в момент времени t₀ будет равно:

(3.5.)