Реферат: Теория автоматического управления
![]() Приравниваем знаменатель передаточной функции замкнутой системы к нулю и записываем характеристическое уравнение:
Приравниваем знаменатель передаточной функции замкнутой системы к нулю и записываем характеристическое уравнение:
Составляем определитель Гурвица:
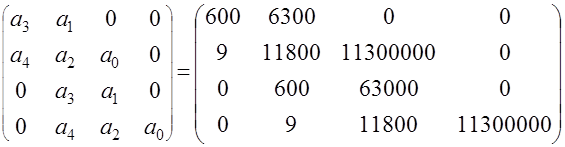 |
??? ????, ????? ???????? ???????????? ??????? ???? ?????????, ?????????? ? ??????????, ????? ??? ???????????? ?????? ???????????? ??????? ? ??? ???????????? ????? ?????, ?????????? ?? ?????? ??????? ???????????? ??????????????????? ?????????, ?.?. ???? ??????????????:
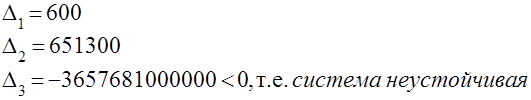
3. Определяем значение критического коэффициента усиления разомкнутой системы, при котором САУ будет находиться на границе устойчивости, с помощью критерия Гурвица
Выпишем знаменатель ПФ в замкнутом состоянии и приравняем его к нулю, получим характеристическое уравнение:
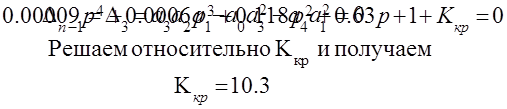
Для определения критического коэффициента приравняем к нулю (n - 1) диагональный минор в определители Гурвица для данного характеристического уравнения и получим выражение:
4. Исследовать влияние одного из параметров системы на устойчивость системы (метод Д-разбиения).
Исследуем влияние параметра T1 на устойчивость системы методом Д-разбиения.
Для получения кривой Д-разбиения решим характеристическое уравнение (знаменатель ПФ в замкнутом состоянии) относительно T1 .
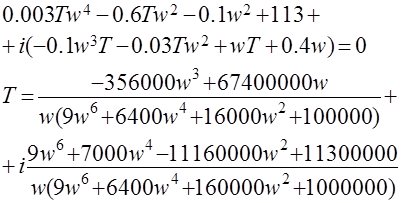 |
Задаваясь частотой –¥ £ w £ +¥ строим кривую Д-разбиения и штрихуем левую сторону кривой при движении по ней с увеличением частоты от –¥ до +¥.
1. В 1 области К правых корней
2. Из 1 во 3 (К+1) правых корней
3. Из 3 во 2 (К+2) правых корней
4. Из 2 в 3 (К+1) правых корней
5. Из 3 в 1 К правых корней
6. Из 1 в 4 (К-1) правых корней
Далее проводим анализ полученных полуплоскостей с точки зрения выделения полуплоскости, претендующей на устойчивость, т.е. такой, которая будет содержать наименьшее число правых корней.
Таким образом, полуплоскость 4 - полуплоскость претендент на устойчивость. Проверим по критерию Гурвица устойчивость для того значения параметра, который находиться внутри полуплоскости - претендента, т.е. в отрезке лежащем на вещественной оси от 19 до +¥.
Расчетная таблица:
| w | P(w) | Q(w) |
| 0 | 67.4 | ¥ |
| 13.76 | 0 | -0.381 |
| -13.76 | 0 | -0.381 |
| 28-3.2*10-19 i | 0.025 | 0 |
| -28+3.2*10-19 i | 0.025 | 0 |
| -8.7*10-19 -40i | -0.031 | -0.00176i |
| 8.7*10-19 +40i | -0.031 | 0.00176i |
| 3.2+2.8*10-18 i | 19 | 0 |
| -3.2-2.8*10-18 i | 19 | 0 |
| ¥ | 0 | 0 |
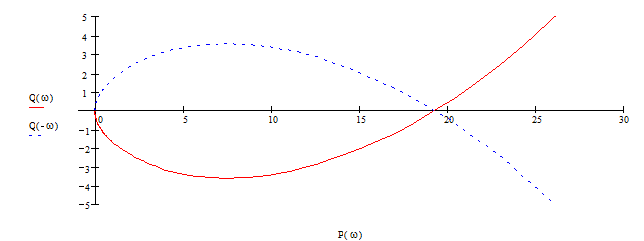
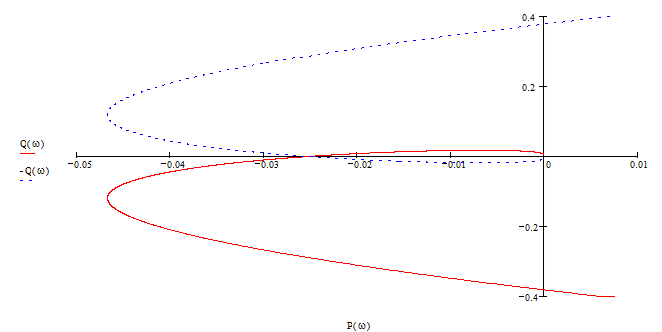
Возьмем T1 =25
Тогда, характеристическое уравнение будет:
![]()
Составляем определитель Гурвица:
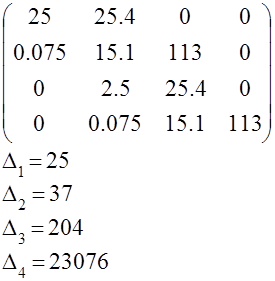 |
Все определители больше нуля значит, система устойчива при 19£T1 £¥.
5.Синтез корректирующего устройства, обеспечивающее требуемые показатели качества в установившемся и переходном режимах.
Синтезируем корректирующее устройство для заданной системы, т.к. согласно п.2 она неустойчива. По заданным показателям качества строим желаемую ЛАХ разомкнутой системы.
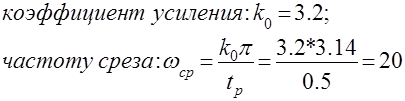 |
?????????? (?? ??????? ??? ??????????? ???????????? K0 ?? ??????????? ?????????????????):
Проводим асимптоту с наклоном -20 дб/дек через частоту среза до пересечения с заданной ЛАХ. В высокочастотной области проводим асимптоту с наклоном –80 дб/дек и получаем желаемую ЛАХ.
Вычитание ЛАХ исходной системы из ЛАХ желаемой системы получаем ЛАХ корректирующего устройства. По полученной ЛАХ подбираем корректирующее устройство, его передаточная функция имеет вид:
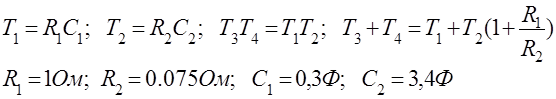 |
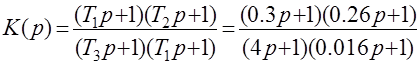 |
Строим структурную схему скорректированной системы:
Записываем ПФ скорректированной системы в разомкнутом и замкнутом состояниях: