Реферат: Теорія подібностей

.

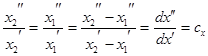Подобным же образом dy=y2-y1 и, следовательно, к нему применимо .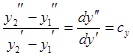

Вообще говоря, подобных друг другу явлений бывает не два, а значительное количество. Мы будем говорить, что они составляют группу подобных явлений.

Сравнивая все члены группы с одним явлением, которое служит образцом для них, замечаем, что при переходе от одного, подобного образца явления к другому, к третьему и т.д. константы подобия каждый раз получают другое значение, сохраняя в то же время свое свойство – быть постоянными во всех точках каждой системы, подобной образцу.

Объединяя переход от явления образца ко всем подобным ему, мы можем рассматривать его выражение как групповое преобразование явления, подразумевая под константой последовательно ее значения для всей группы подобных образцу величин.

Подобие явлений можно выразить и другим способом: не константами подобия, а посредством так называемых инвариантов подобия.

Перейдем от абсолютной системы единиц, общей для всех явлений данного класса, к относительной системе, пригодной только для одного явления этого класса. Для этого выберем за единицы измерения величин рассматриваемой системы значения этих величин в каких-нибудь точках самой системы. Отметим их подстрочным индексом (0). Тогда все величины и другие для первого явления получат численные значения:

и т.д.

Если во втором явлении за единицы измерения величин выбрать их значения в сходственных первой системе точках, то их значения в относительных единицах будут

и.т.д.

Очевидно, и т. д. будут те же, что и в первой системе.

В самом деле легко видеть, что

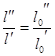и. т. д.

Переставляя члены пропорции, получим

.

То же самое получится для любых других величин, характеризующих подобные явления.

Поэтому значки, отмечающие, к какому из явлений относятся величины L, W и т. д., можно отбросить, так как при переходе от одного явления к другому, ему подобному, все величины, выраженные в относительных единицах измерения, останутся численно прежними.

Иными словами, они являются инвариантами подобия. Будем обозначать это свойство их словами іnv. (инвариант) или іdem (то же самое).

Следовательно, L=idem, W=idem или для общего случая .

Следует уметь хорошо отличить понятия «константа подобия» и «инвариант подобия».

Константа сохраняет постоянное значение во всех точках системы, но она делается другой, когда одна пара подобных явлений заменяется другой.

Инвариант подобия, наоборот, различен для разных точек системы, поскольку он изображает одну из величин этой системы, имеющую разное численное значение в разных точках системы; но он не меняется при переходе от одного явления к любому другому, подобному ему. Иначе говоря, он сохраняет одно и то же значение в сходственных точках всей группы подобных явлений.

В дальнейшем мы будем пользоваться определением подобия и через константы, и через инварианты в зависимости от того, какое определение при рассмотрении различных вопросов оказывается удобнее в смысле простоты изложения.

Возвращаясь к определению подобия через константы подобия, отметим, что на первый взгляд выбор всех констант подобия может казаться произвольным. На самом деле это не так. Величины, характеризующие различные явления, не являются независимыми друг от друга. Часто между ними существует определенная связь. Эта связь, называемая законом природы, во многих случаях может быть выражена в математической форме в виде уравнения.

Наличие такого уравнения, делающего одни величины зависимыми от других, налагает и на константы подобия определенные ограничения.

Нахождение зависимости между константами подобия, вызываемой существованием уравнения, связывающего между собой характеризующие явление величины, составляет содержание теоремы подобия, которая будет изложена в следующей главе.

Уравнения, описывающие различные явления природы, можно рассматривать, как имеющие различную степень общности.