Реферат: Теорія подібностей

Исследование на моделях позволяет ускорить или замедлить процессы, которые в натурных условиях развиваются со скоростью, затрудняющих вести наблюдение. При проведении эксперимента непосредственно на натуре почти всегда приходится отказываться от активного поиска оптимальных конструктивных решений, ибо это связано со значительными денежными затратами, а не редко и просто не возможно.

Теория моделирования базируется на принципах, вытекающих из теории подобия. Эти принципы заключаются в соблюдении условий, которые определяют соотношения между параметрами модели и натуры, а так же правила пересчета исследуемых величин с модели на натуру и обратно. Однако, известно, что ни одна модель не может с абсолютной полнотой воспроизвести изучаемый оригинал – для этого должно быть полное их тождество. Поэтому при моделировании стараются соблюсти в модели по крайней мере те характеристики натуры, которые являются наиболее существенными в общей картине физического процесса, обеспечивая заданную точность результатов (например при расчете стержневых конструкций пренебрегают собственным весом, а при проектировании плотины насыпи рассматривают как распределенную нагрузку).

Методы подобия в механике.

Движение математического маятника

В качестве первого примера мы рассмотрим классический пример о движении математического маятника.

Математический маятник (рис. 1) представляет собой тяжелую материальную точку, подвешенную на невесомой и нерастяжимой нити, которая закреплена другим своим концом неподвижно. Совокупность возможных движений мы ограничим условием, что движения маятника плоские.

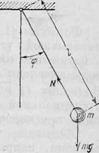
Рис. 1. Математический маятник.

Введем обозначения: l — длина маятника, φ — угол между нитью и вертикалью, t — время, m — масса груза и N — натяжение нити. Если пренебречь силами сопротивления, то задача о движении маятника приводится к решению уравнений

, (1)

(2)

с начальным условием

при t=0 φ=φ0 и ,

т. е. за начальный момент времени принят тот момент, когда маятник отклонен на угол φ0, а скорость равна нулю.

Из уравнений (1), (2) и начального условия очевидно, что в качестве определяющих параметров можно взять следующую систему:

t, l, g, m, φ0.

Числовые значения всех остальных величин определяются полностью значениями этих параметров. Следовательно, мы можем написать

φ = φ (t, φ0, l, g, m), N=mgf(t, φ0, l, g, m) (3)

где φ и f – безразмерные величины.

Числовые значения функций φ и f не должны зависеть от системы единиц измерения. Вид этих функций можно определить либо решая уравнения (1) и (2), либо экспериментальным способом.

Из общих соображени