Реферат: Теория вектора

Задача 2.

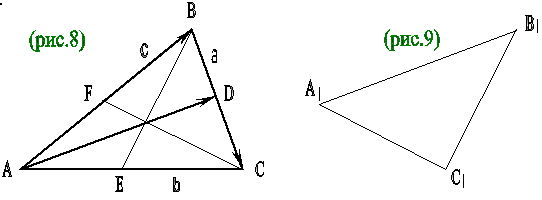
Дан произвольный треугольник АВС. Доказать, что можно построить треугольник, стороны которого равны и параллельны медианам треугольника АВС.

Решение.

Обозначим медианы треугольника АВС через ВЕ, СF и обозначим векторы, идущие вдоль сторон треугольника АВС, через а, в, с :

ВС = а, СА = в, АВ = с

(рис.8). Тогда

АD = АВ + ВD = АВ += с +

аналогично определяются и другие медианы:

ВЕ = а + , СF = в +

Так как, в силу условия замкнутости

ВС + СА + АВ = а + в + с = 0,

то мы имеем:

АD + ВЕ + СF = ( с + ) + (а + ) + ( в + ) = ( а + в + с ) = х 0 = 0.

Следовательно, отложив от точки В, вектор В₁ С₁ = ВЕ и от точки С₁ – вектор С₁ D₁ = СF, мы получим.

А₁ В₁ + В₁ С₁ + С₁ D₁ = АD + ВЕ + СF = 0.

А это значит (в силу условия замкнутости), что ломаная А₁ В₁ С₁ D₁ является замкнутой, т.е. точка D₁ совпадает с А₁ .

Таким образом, мы получаем треугольник А₁ В₁ С₁ (рис.9), стороны которого равны и параллельны медианам АD, ВЕ, СF исходного треугольника.

Задача 3.

Доказать, что для любого треугольника имеет место формула

с² = а² + в² – 2ав х соs С (теорема косинусов)

Решение.

Положим: а = СВ, в = СА,

с = АВ (рис.10).

Тогда с = а – в , и мы имеем

(учитывая, что угол между векторами а и в равен С):

с² = ( а – в )² = а² – 2ав + в² = а² – 2ав х соs С + в² .

Задача 4.

Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

Решение.

Пусть четырехугольник АВСD – параллелограмм (рис.11). Имеем векторные равенства

АВ + AD = АС, АВ – АD = DВ.

Возведем эти равенства в квадрат. Получим:

АВ² + 2 АВ х АD + АD² = АС² , АВ² – 2АВ х АD + АD² = DВ²

Сложим эти равенства почленно. Получим:

2АВ² + 2 АD² = АС² + DВ² .

Так как у параллелограмма противолежащие стороны равны, то это равенство и означает, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон, что и требовалось доказать.

Задача 5.

Даны три точки: А ( 1; 1), В ( -1; 0), С ( 0; 1). найдите такую точку D ( х; y ), чтобы векторы АВ и СD были равны.