Реферат: Теплопроводность в сплошных средах и двухфазных, продуваемых и непродуваемых телах (слоях).

Одной из наиболее простых и физически обоснованных является модель, предложенная Кунии.

В этой модели рассматривается осесимметричный тепловой поток между плоскостями, проходящими через центры двух соседних шаров. С учетом всех механизмов переноса теплоты в зернистом слое была получена формула.

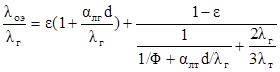
(III),

в которой:

-коэффициент теплоотдачи излучением от зерна через газ мимо соседних зерен

-коэффициент теплоотдачи излучением между соседними зернами; p - степень черноты поверхности зерен

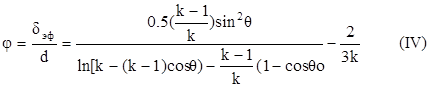F - ??? ????????????? ??????????? ??????? ??????? ????????? ????? ??????:

где k=l_т /l_г ; q - центральный угол, приходящийся на одну точку контакта (зависит от геометрической укладки шаров).

Таким образом, в формуле (III) первый член учитывает тепловой поток через газовую фазу теплопроводностью и излучением, а второй член - теплопередачу через зерна за счет контактного и лучистого теплообмена между ними.

Сравнение расчетов по формуле (III) с опытными данными разных исследователей проведено во многих работах. В широком диапазоне изменения размеров зерен и порозности слоя для разных газов, жидкостей и материала зерен получено хорошее совпадение результатов.

Модель теплопроводности зернистого слоя, не учитывающая передачу теплоты излучением

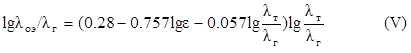??? ?????? ??????????? (<300⁰ ?), ????? ???? ???????? ????? ?????????? ????, ????? ???????????? ???????????????? ????????:

В этой формуле коэффициенты подобраны в результате сравнения с опытными данными для 163 укладок. При этом разброс опытных данных l_оэ /l_г =1-40 лежит, в основном, в пределах ±30%. Формула (V) получена без учета переноса теплоты излучением.

Необходимо учитывать, что при температуре выше 300^о С доля переноса теплоты излучением в зернистом слое становится заметной. Так, при отношении теплопроводностей фаз l_т /l_г »100 и e»0.4 значение l_оэ /l_г »8-10 (при температуре до 100^о С). С увеличением температуры до 600^о С это значение возрастает вдвое, а при 800^о С-втрое. Естественно, в этом случае формула (V) неприменима

Теплопроводность в зернистом слое в условиях естественной конвекции

При наличии градиента температуры в зернистом слое, заполненном жидкостью или газом достаточно большой плотности, может возникнуть естественная конвекция, приводящая к заметному увеличению эффективного коэффициента теплопроводности.

С возможностью естественной конвекции нужно считаться при процессах горения в шахтных топках и газогенераторах, при каталитических процессах в начальных участках реакторов с большим градиентом темепратуры и концентрации, в доменных печах, в тепловой изоляции в виде зернистой засыпки.

Рассмотрим зернистый слой высотой x , имеющий температуру верхнего торца t₂ и нижнего торца t₁ , причем t₁ >t₂ . При отсутствии конвективных потоков газа в слое установится одномерный тепловой поток q, определяемый коэффициентом теплопроводности l_оэ при линейном распределении температуры по высоте слоя. Примем далее, что в направлении, одинаковом с направлением теплового потока, движется поток газа (жидкости) с массовой скоростью G; распределение температуры по высоте слоя остается неизменным и одинаковым для обеих фаз. Такое допущение оправдано, если основное количество теплоты передается теплопроводностью. Конвективный тепловой поток:

q_к =С_p G(t₁ -t₂ ) (VI)

Конвективная составляющая коэффициента теплопроводности описывается выражением:

l_к =q_к /(t₁ -t₂ )/x=C_p Gx (VII)

а суммарная теплопроводность слоя при наличии конвекции равна:

l_э =l_оэ +l_к (VIII)

В рассматриваемом случае естественная конвекция в слое вызвана различием плотности газа за пределами слоя при t₂ и средней плотности в слое при температуре 0.5(t₁ +t₂ ).

Dr=0.5rb_t Dt (IX)

где b_t - коэффициент объемного расширения газа; Dt =t₁ -t₂ .

???????? ???? ???????? ?????? Dp=?Drg ???????????????? ? ????, ??????? ??? ?????????? ??????? ???????? ?????????? ????????????:
?? ???? ??????????? ?????:

где С=e³ /a² K - коэффициент проницаемости слоя, зависящий от его структуры.

????? ????????? ?????????????? ????????:

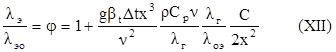Здесь:

- критерий Грасгофа, отнесенный к разнице температур в слое; в качестве определяющего размера принята высота слоя;

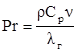
- критерий Прандтля для газовой среды;

- критерий Релея для зернистого слоя.

В отличие от аналогичного критерия GrPr, применяемого для описания естественной конвекции в однофазной среде, а Ra входят два симплекса, отражающие тепловые и гидравлические свойства зернистого слоя.