Реферат: Тепловидение

λ,м

Т₁ > Т₂ > Т₃

Экспериментальные кривые зависимости испускательной способности абсолютно черного тела от длины волны и температуры.

Из рисунка следует, что энергетическая светимость абсолютно черного тела сильно возрастает с температурой.максимум испускательной способности с увеличением температуры сдвигается в сторону более коротких волн.

Т.о., по закону Кирхгофа функция частоты и температуры f(ω,Т) есть не что иное, как испускательная способность абсолютно черного тела (r ч.т.).

r/а = f(ω,Т) а ч.т.≡1 r ч.т.= f(ω,Т)

3. Классические законы теплового излучения

Исследование равновесного теплового излучения и поиск универсальной функции f(ω,Т) выступил на первый план в работах физиков конца XIX века.

К этим исследованиям относятся работы Стефана и Больцмана, Рэлея и Джинса, Вина (классическая теория излучения) и Планка (квантовая).

В 1879 г. Йозеф Стефан, основываясь на экспериментах, решил, что энергетическая светимость любого тела пропорциональна четвертой степени температуры. Однако через несколько лет Больцман доказал, что это утверждение справедливо только для абсолютно черных тел. Найденная ими зависимость получила названия закона Стефана-Больцмана.

R ч.т.= ∫ f(ω,T)·dω = σ·Т⁴ ,где σ экспериментально найденная константа.

σ = 5,670·10^-8 (Вт/м²·К)

Вилли Вин нашел зависимость температуры абсолютно черного тела от максимума спектра излучения (λmax). Оказалось, что с повышением температуры возрастает общая энергия излучения, а максимум спектра излучения смещается в область меньших длин волн (высоких частот).

ҷλ max= const

(const = 2,898 10 м·К – экспериментальное значение)

Этот закон называют законом смещения Вина.

Вин также занимался поиском функции спектрального распределения f(ω,Т) и нашел, что она должна иметь следующий вид: f(ω,T) = ω³F(ω/Т), где F – некоторая функция отношения частоты к температуре. Как будет показано ниже, эта формула справедлива только для больших частот.

Введем понятие плотности равновесного теплового излучения (u), т.е. энергии, испускаемой в данном интервале частот (от ω до ω+dω).

d u (ω,T)= f(ω,T) ·d ω

Рэлей и Джинс сделали попытку определить зависимость плотности излучения u от ω и Т, исходя из теоремы классической статистики о равнораспределении энергии по степеням свободы. Они предположили, что на каждое электромагнитное колебание приходится в среднем энергия, равная kТ: kТ/2 на электрическую и kТ/2 на магнитную энергию волны.

Они получили:

??? ??????? ????????????????? ??????????? ? ????????????? ?????? ? ??????? ????? ?????? (???????????? ???????) ? ????? ?????????? ? ???????????????? ???????. ?? ?? ??????? ?????????, ??? ?????????? ??????????? ?????? ???? ?????? ?????? ??? ???? ??????? ????????? ? ?????????? ?? ??????????? ????. ???? ????? ??? ?????? ???????????????? ???????????.

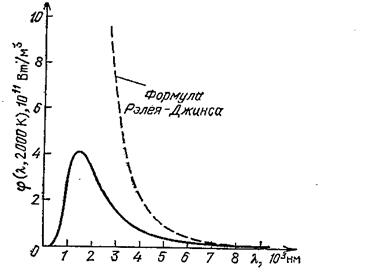
Кривые зависимости испускательной способности φ(λ) абсолютно черного тела от длины волны. Сплошная кривая получена экспериментально, штриховая кривая построена по формуле Рэлея-Джинса. Из графика видно, что при λ→0 (ω→∞) r(ω,T)→∞.

С точки зрения классической теории излучения вывод формулы Рэлея-Джинса безупречен. Поэтому расхождение этой формулы с опытом указывало на существование каких-то закономерностей, несовместимых с представлениями классической физики.

4. Понятие о квантах. Формула Планка и вывод из нее классических законов как частных случаев

19 октября 1900 года на заседании физического общества в Берлине Макс Планк предложил свою формулу, которая, как он считал, помогала устранить вышеописанные несоответствия.

Тогда он нашел ее полуэмпирическим путем, и только в процессе ее теоретического обоснования обнаружил, что это уравнение справедливо только при допущении, что энергия может излучаться и поглощаться не непрерывно, а лишь в известных неделимых порциях – квантах (квант энергии – «ε»; ε = ћω, где ћ – постоянная Планка; ћ =1,0546 ·10^-3 Дж·с).

В отличие от классического осциллятора, энергия которого равна КТ, энергия квантового равна ћω/exp(ћω/КТ) – 1.

Итак, Планку удалось найти универсальную f(ω,Т), в точности согласующуюся с опытами: