Реферат: ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ

Следовательно, в случае, когда давление остается постоян­ным, количество получаемой телом теплоты равно прира­щению энтальпии.

Дифференцирование выражения (21) с учетом (5) дает

(24)

Отсюда заключаем, что энтальпия есть термодинамиче­ская функция в переменных S и р. Её частные произ­водные равны

(25)

В соответствии с (22) теплоемкость при постоянном давлении

(26)

Таким образом, если объем системы остается постоянным, то тепло Q равно приращению внутренней энергии системы. Если же постоянно давление, то оно выражается приращением энтальпии. В обоих случаях величина Q не зависит от пути перехода, а только от начального и конечного состояний системы. Поэтому на основании опытов при постоянном объеме или при постоянном давлении и могло сложиться представление о какой-то величине Q , содержа­щейся в теле и не зависящей от способа приведения его из нуле­вого состояния в рассматриваемое. Величина Q имеет различный смысл в зависимости от того, что остается постоянным: объем или давление. В первом случае под Q следует понимать внутреннюю энер­гию, во втором — энтальпию. Но в ранних опытах это различие ускользало от наблюдений, так как опыты производились с твердыми и жидкими телами, для которых оно незначительно благодаря малости коэффициентов теплового расширения твердых и жидких тел. В обоих случаях имеет место сохранение величины Q , но оно сводится к закону сохранения энергии.

В таблице приведены основные свойства термодинамических функций.

Название и обозначение термодинамической функции	Свойства
Внутренняя энергия		при адиабатическом процессе
		при
Свободная энергия		при обратимом изотермическом процессе
		для равновесного состояния при и
Энтальпия		при
Термодинамический потенциал Гиббса		для равновесного состояния при и

6. Некоторые термодинамические соотношения

Итак, мы получили соотношения

(27)

(28)

(29)

(30)

Отсюда

(31)

(32)

(33)

(34)

Отметим два следствия выведенных уравнений. Из определения функций F и G следует . Подставив сюда выражения для энтропии из формул (33) и (34), получим

(35)

(36)

Эти уравнения называются уравнениями Гиббса — Гельмгольца . Сразу можно отметить пользу, которую можно извлечь из этих уравнений. Часто бывает легко найти свободную энергию F с точностью до слагаемого, зависящего только от температуры. Это можно сде­лать, вычислив изотермическую работу, совершаемую системой. Тогда формула (35) позволяет с той же неопределенностью найти и внутреннюю энергию системы.

Если известна функция , то дифференцированием ее по S и V можно найти температуру и давление системы, т. е. полу­чить полные сведения о ее термических свойствах. Затем по фор­муле можно найти и соответствующие теплоемкости, т. е. получить полные сведения также и о калорических свойствах системы. То же самое можно сделать с помощью любого из оставших­ся трех канонических уравнений состояния.

Далее, вторичным дифференцированием из соотношений (31) находим

Отсюда на основании известной теоремы анализа о перемене порядка дифференцирования следует

(37)

Аналогично,

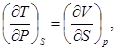(38)

(39)

(40)

Эти и подобные им соотношения называются соотношениями вза­имности или соотношениями Максвелла . Они постоянно исполь­зуются для вывода различных соотношений между величинами, характеризующими термодинамически равновесные состояния си­стемы. Такой метод вывода называется методом термодинами­ческих функций или термодинамических потенциалов.