Реферат: Термодинамика

Функция состояния , выражаемая уравнениями .

Пространственно - временная структура , возникающая из-за неустойчивости .

Флуктуации , ответственные за неустойчивости .

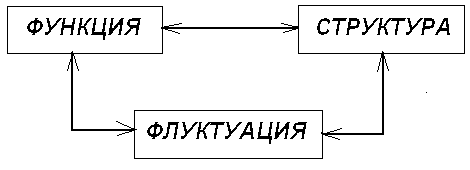
Рис. 1. Три аспекта диссипативных структур.

Взаимодействия между этими аспектами приводит к неожиданным явлениям - к возникновению порядка через флуктуации , формированию высокоорганизованной структуры из хаоса.

Таким образом , в диссипативных структурах происходит становление из бытия , формируется возникающее из существующего.

САМООРГАНИЗАЦИЯ РАЗЛИЧНЫХ СТСТЕМ И

СЕНЕРГЕТИКА.

Переход от хаоса к порядку , происходящий при изменении значений параметров от до критических к сверхкритическим , изменяет симметрию системы . По этому такой переход аналогичен термодинамическим фазовым переходам . Переходы в неравновесных процессах называются кинетическими фазовыми переходами . В близи неравновесных фазовых переходов не существует непротиворечивого макроскопического описания . Флуктуации столь же важны , как и среднее значении . Например , макроскопические флуктуации могут приводить к новым типам не устойчивостей .

Итак , в дали от равновесия между химической , кинетической и пространственно-временной структурой реагирующих систем существует неожиданная связь . Правда , взаимодействие , определяющие взаимодействие констант скоростей и коэффициентов переноса , обусловлены короткодействующими силами ( силами валентности , водородными связями и силами Ван-Дер-Вальса) . Однако решения соответствующих уравнений зависят , кроме того , от глобальных характеристик . Для возникновения диссипативных структур обычно требуется , чтобы размеры системы превышали некоторое критическое значение - сложную функцию параметров , описывающих реакционно-диффузионные процессы . Мы можем по этому утверждать , что химические неустойчивости задают дальнейший порядок , посредством которого система действует как целое .

Если учесть диффузию , то математическая формулировка проблем , связанных с диссипативными структурами , потребует изучении дифференциальных уравнений в частных производных . Действительно , эволюция концентрации компонент Х со временем определяется уравнением вида

(2.4)

где первый член дает вклад химических реакций в изменении концентрации Х_i и обычно имеет простой полиноминальный вид , а второй член означает диффузию вдоль оси r.

По истине поразительно , как много разнообразных явлений описывает реакционно-диффузное уравнение (2.4 ) , по этому интересно рассмотреть ² основное решение ² , которое бы соответствовала термодинамической ветви . Другие решения можно было бы получать при последовательных не устойчивостях , возникающих по мере удаления от состояния равновесия . Неустойчивости такого типа удобно изучать методами теории бифуркации [ Николис и Пригожин , 1977] . В принципе , бифуркация есть нечто иное , как возникновение при некотором критическом значении параметра нового решения уравнений . Предположим , что мы имеем химическую реакцию , соответствующую кинетическому уравнению [ Маклейн и Уолис , 1974] .

d X

¾ = a X (X-R) (2.5)

d t

Ясно что при R < 0 существует только одно решение , независящее от времени , X = 0 . В точке R = 0 происходит бифуркация , и появляется новое решение X = R .

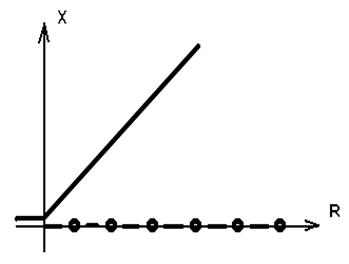
Рис. 2.3. Бифуркационная диограмма для уравнения ( 2.5.) .

Сплошная линия соответствует устойчивой ветви ,

точки - неустойчивой ветви .

Анализ устойчивости в линейном приближении позволяет проверить , что решение X = 0 при переходе через R = 0 становится неустойчивым , а решение X = R - устойчивым . В общем случаи при возрастании некоторого характеристического параметра р происходят последовательные бифуркации . На рисунке 2.4. показано единственное решение при р = р ₁ , но при

р = р ₂ единственность уступает место множественным решения .

Интересно отметить , что бифуркация в некотором смысле вводит в физику и в химию , историю - элемент , который прежде считался прерогативой наук занимающихся изучением биологическим , общественных и культурных явлений .

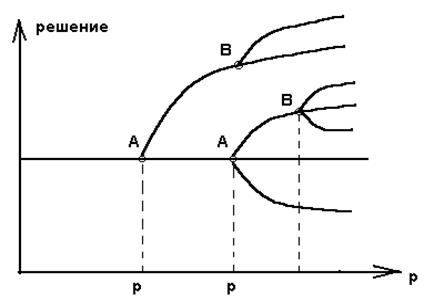
Рис. 2.4. Последовательные бифуркации :

А и А ¹ - точки первичных бифуркаций из

термодинамической ветви ,

В и В ¹ - точки вторичной бифуркации .

Известно , что при изменении управляющих параметров в системе наблюдаются разнообразные переходные явления . Выделим теперь из этих наблюдений определенные общие черты , характерные для большого числа других переходов в физико химических системах .

С этой целью представим графически (рис. 2.5) зависимость вертикальной компоненты скорости течения жидкости в некоторой определенной точке от внешнего ограничения , или , в более общем виде , зависимость переменной состояние системы Х (или х = Х - Х_s ) от управляющего параметра l . Таким образом мы получим график , известный под названием бифуркационной диаграммы .

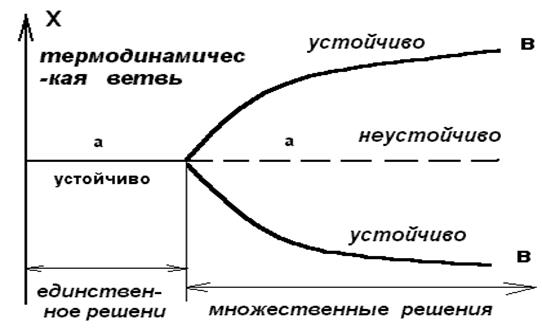
Рис. 2.5. Бифуркационная диаграмма :

а - устойчивая часть термодинамической ветви ,