Реферат: Типовой расчет графов

2-й шаг

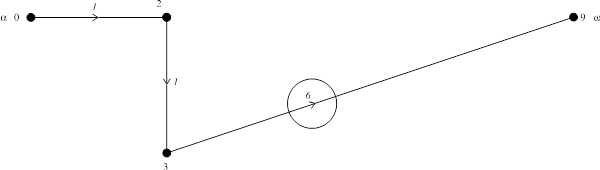
3-й шаг

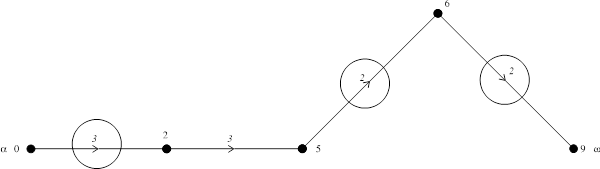
4-й шаг

5-й шаг

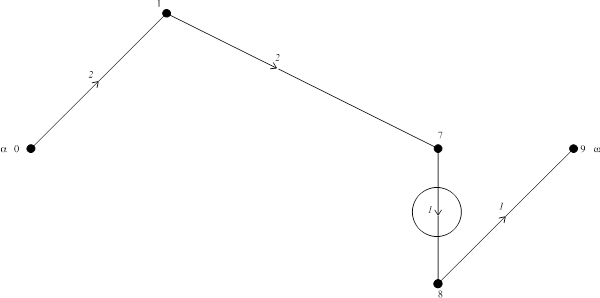
6-й шаг

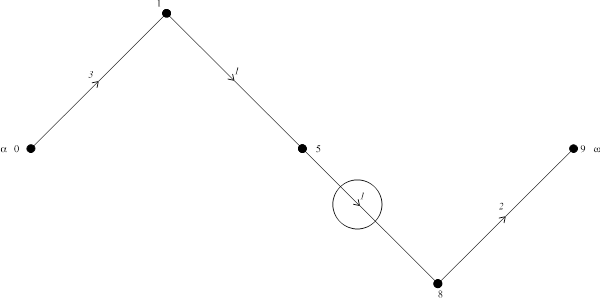
7-й шаг

Окончательно имеем:

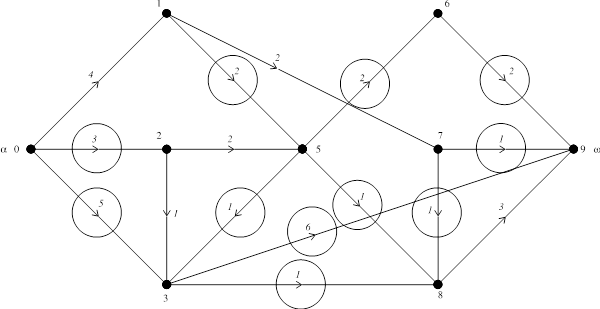
Как видно из рисунка, ребра {6,9},{7,9},{3,9}, питающие вершину w, насыщенны, а оставшееся ребро {8,9}, питающееся от вершины 8, не может получить большее значение весовой функции, так как насыщенны все ребра, питающие вершину 8. Другими словами - если отбросить все насыщенные ребра, то вершина w недостижима, что является признаком максимального потока в сети.

Максимальный поток в сети равен 12.

Минимальный разрез сети по числу ребер: {{0,1},{0,2},{0,3}}. Его пропускная способность равна 16

Минимальный разрез сети по пропускной способности: {{6,9}, {7,9}, {3,9}, {3,8}, {5,8}, {7,8}}. Его пропускная способность равна 12.

Задача 7 (Задача о почтальоне) Выписать степенную последовательность вершин графа G.

а) Указать в графе G Эйлерову цепь. Если таковой цепи не существует, то в графе G добавить наименьшее число ребер таким образом, чтобы в новом графе можно было указать Эйлерову цепь.

б) Указать в графе G Эйлеров цикл. Если такого цикла не существует, то в графе G добавить наименьшее число ребер таким образом, чтобы в новом графе можно было указать Эйлеров цикл.

Степенная последовательность вершин графа G:

(3,6,4,5,3,6,4,3,4,4)

а) Для существования Эйлеровой цепи допустимо только две вершины с нечетными степенями, поэтому необходимо добавить одно ребро, скажем между вершинами 4 и 7.

Полученная Эйлерова цепь: 0,3,2,0,1,2,5,1,4,5,6,1,7,4,6,9,7,8,9,3,8,5,3.

Схема Эйлеровой цепи (добавленное ребро показано пунктиром):

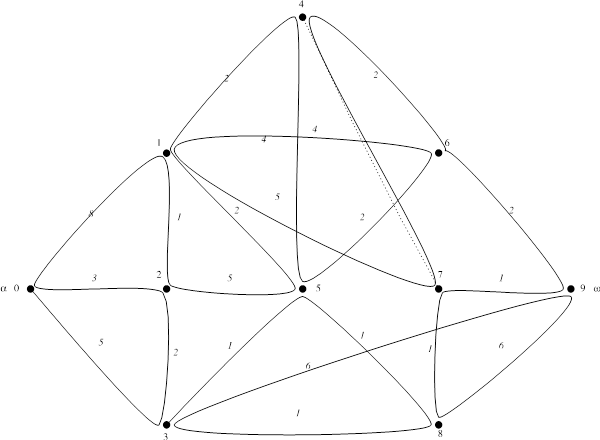
б) Аналогично пункту а) добавляем ребро {3,0}, замыкая Эйлерову цепь (при этом выполняя условие существования Эйлерова цикла - четность степеней всех вершин). Ребро {3,0} кратное, что не противоречит заданию, но при необходимости можно ввести ребра {0,7} и {4,3} вместо ранее введенных.