Реферат: Типовой расчет графов
Схема Эйлерова цикла (добавленные ребра показаны пунктиром):
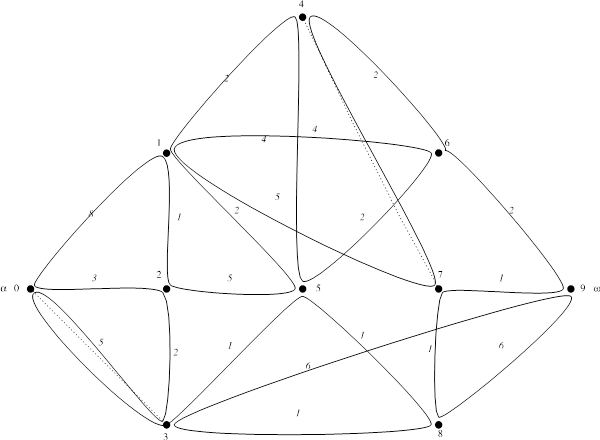
Задача 8
а) Указать в графе Gор Гамильтонов путь. Если такой путь не существует, то в графе Gор изменить ориентацию наименьшего числа ребер таким образом, чтобы в новом графе Гамильтонов путь можно было указать.
б) Указать в графе Gор Гамильтонов цикл. Если такой цикл не существует, то в графе Gор изменить ориентацию наименьшего числа ребер таким образом, чтобы в новом графе Гамильтонов цикл можно было указать.
а) Гамильтонов путь (ребра с измененной ориентацией показаны пунктиром):
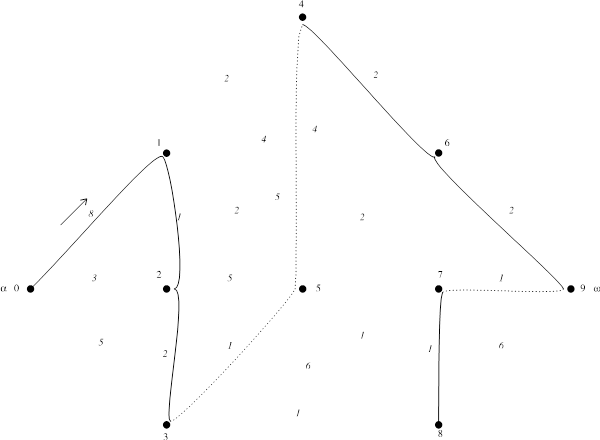
б) Гамильтонов цикл (ребра с измененной ориентацией показаны пунктиром):
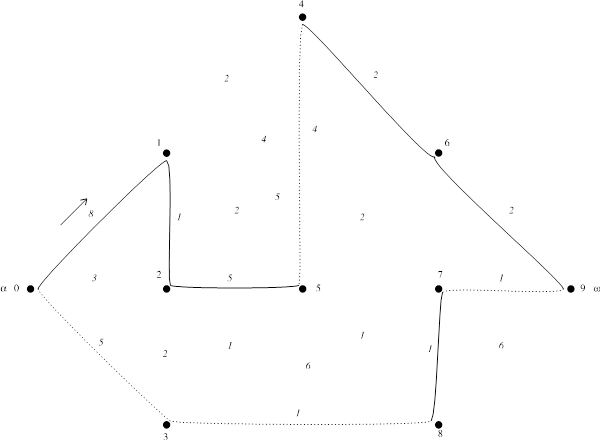
Задача 9 (Задача о коммивояжере) Дан полный ориентированный симметрический граф 
с вершинами x1, x2,...xn.Вес дуги xixj задан элементами Vij матрицы весов. Используя алгоритм метода ветвей и границ, найти Гамильтонов контур минимального (максимального) веса. Задачу на максимальное значение Гамильтонова контура свести к задаче на минимальное значение, рассмотрев матрицу с элементами 
,где 
. Выполнить рисунок.
Исходная таблица.
| x1 | x2 | x3 | x4 | x5 | x6 | |
| x1 | ¥ | 3 | 7 | 2 | ¥ | 11 |
| x2 | 8 | ¥ | 06 | ¥ | 4 | 3 |
| x3 | 6 | 05 | ¥ | 7 | ¥ | 2 |
| x4 | 6 | ¥ | 13 | ¥ | 5 | ¥ |
| x5 | 3 | 3 | 3 | 4 | ¥ | 5 |
| x6 | 8 | 6 | ¥ | 2 | 2 | ¥ |
Таблица Е 
14
| x1 | x2 | x3 | x4 | x5 | x6 | ||
| x1 | ¥ | 1 | 5 | 01 | ¥ | 7 | 2 |
| x2 | 8 | ¥ | 01 | ¥ | 4 | 1 | |
| x3 | 6 | 00 | ¥ | 7 | ¥ | 00 | |
| x4 | 1 | ¥ | 8 | ¥ | 01 | ¥ | 5 |
| x5 | 01 | 00 | 00 | 1 | ¥ | 00 | 3 |
| x6 | 6 | 4 | ¥ | 00 | 00 | ¥ | 2 |
| 2 |
Дробим по переходу x2-x3:
Таблица 
23 å=14+0=14
| x1 | x2 | x4 | x5 | x6 | |
| x1 | ¥ | 1 | 01 | ¥ | 7 |
| x3 | 6 | ¥ | 7 | ¥ | 06 |
| x4 | 1 | ¥ | ¥ | 01 | ¥ |
| x5 | 01 | 01 | 1 | ¥ | 00 |
| x6 | 6 | 4 | 00 | 00 | ¥ |
Таблица 
23 å=14+1=15
| x1 | x2 | x3 | x4 | x5 | x6 | ||
| x1 | ¥ | 1 | 5 | 01 | ¥ | 7 | |
| x2 | 7 | ¥ | ¥ | ¥ | 3 | 03 | 1 |
| x3 | 6 | 00 | ¥ | 7 | ¥ | 00 | |
| x4 | 1 | ¥ | 8 | ¥ | 01 | ¥ | |
| x5 | 01 | 00 | 05 | 1 | ¥ | 00 | |
| x6 | 6 | 4 | ¥ | 00 | 00 | ¥ |
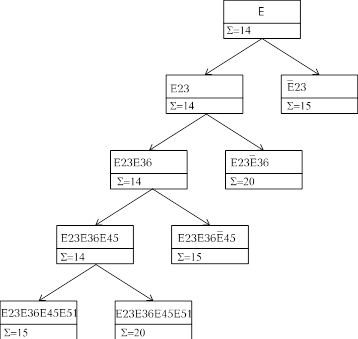
Продолжаем по 23. Дробим по переходу x3-x6:
Таблица 23E36 å=14+0=14
| x1 | x2 | x4 | x5 | |
| x1 | ¥ | 1 | 01 | ¥ |
| x4 | 1 | ¥ | ¥ | 01 |
| x5 | 01 | 01 | 1 | ¥ |
| x6 | 6 | ¥ | 00 | 00 |
Таблица 2336 å=14+6=20
| x1 | x2 | x4 | x5 | x6 | ||
| x1 | ¥ | 1 | 01 | ¥ | 7 | |
| x3 | 01 | ¥ | 1 | ¥ | ¥ | 6 |
| x4 | 1 | ¥ | ¥ | 01 | ¥ | |
| x5 | 00 | 01 | 1 | ¥ | 07 | |
| x6 | 6 | 4 | 00 | 00 | ¥ |
Продолжаем по 2336. Дробим по переходу x4-x5:
Таблица 23E3645 å=14+0=14
| x1 | x2 | x4 | |
| x1 | ¥ | 1 | 01 |
| x5 | 01 | 01 | 1 |
| x6 | 6 | ¥ | 00 |
Таблица 2336
45 å=14+1=15
| x1 | x2 | x4 | x5 | ||
| x1 | ¥ | 1 | 01 | ¥ | |
| x4 | 00 | ¥ | ¥ | ¥ | 1 |
| x5 | 01 | 01 | 1 | ¥ | |
| x6 | 6 | ¥ | 00 | 00 |
Продолжаем по 233645. Дробим по переходу x5-x1:
Таблица 23364551 å=14+1=15
| x2 | x4 | ||
| x1 | 1 | ¥ | 1 |
| x6 | ¥ | 00 |
Таблица 23364551 å=14+6=20
| x1 | x2 | x4 | |
| x1 | ¥ | 1 | 01 |
| x5 | ¥ | 01 | ¥ |
| x6 | 0 | ¥ | 00 |
| 6 |
Окончательно имеем Гамильтонов контур: 2,3,6,4,5,1,2.
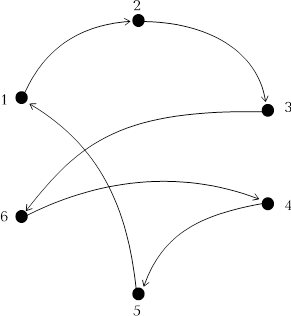
Прадерево разбиений:
Задача 10 (Задача о назначениях) Дан полный двудольный граф Knn с вершинами первой доли x1, x2,...xn.и вершинами другой доли y1, y2,...yn..Вес ребра {xi,yj} задается элементами vij матрицы весов. Используя венгерский алгоритм, найти совершенное паросочетание минимального (максимального веса). Выполнить рисунок.