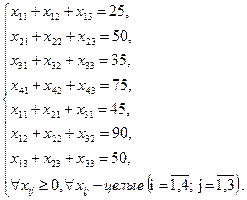Реферат: Транспортная задача 2
В случае, когда суммарные запасы превышают суммарные потребности , необходим дополнительный фиктивный пункт потребления, который будет формально потреблять существующий излишек запасов, то есть:
| (8) |
Если суммарные потребности превышают суммарные запасы , то необходим дополнительный фиктивный пункт отправления, формально восполняющий существующий недостаток продукции в пунктах отправления:
| (9) |
Введение фиктивного потребителя или отправителя повлечет необходимость формального задания фиктивных тарифов ![]() (реально не существующих) для фиктивных перевозок. Поскольку нас интересует определение наиболее выгодных реальных перевозок, то необходимо предусмотреть, чтобы при решении задачи (при нахождении опорных планов) фиктивные перевозки не рассматривались до тех пор, пока не будут определены все реальные перевозки. Для этого надо фиктивные перевозки сделать невыгодными, то есть дорогими, чтобы при поиске решения задачи их рассматривали в самую последнюю очередь. Таким образом, величина фиктивных тарифов должна превышать максимальный из реальных тарифов, используемых в модели, то есть
(реально не существующих) для фиктивных перевозок. Поскольку нас интересует определение наиболее выгодных реальных перевозок, то необходимо предусмотреть, чтобы при решении задачи (при нахождении опорных планов) фиктивные перевозки не рассматривались до тех пор, пока не будут определены все реальные перевозки. Для этого надо фиктивные перевозки сделать невыгодными, то есть дорогими, чтобы при поиске решения задачи их рассматривали в самую последнюю очередь. Таким образом, величина фиктивных тарифов должна превышать максимальный из реальных тарифов, используемых в модели, то есть
| (10) |
На практике возможны ситуации, когда в определенных направлениях перевозки продукции невозможны, например, по причине ремонта транспортных магистралей. Такие ситуации моделируются с помощью введения так называемых запрещающих тарифов ![]() . Запрещающие тарифы необходимо сделать невозможными, то есть совершенно невыгодными, перевозки в соответствующих направлениях. Для этого величина запрещающих тарифов должна превышать максимальный из реальных тарифов, используемых в модели:
. Запрещающие тарифы необходимо сделать невозможными, то есть совершенно невыгодными, перевозки в соответствующих направлениях. Для этого величина запрещающих тарифов должна превышать максимальный из реальных тарифов, используемых в модели:
| (11) |
2. Решение сбалансированной транспортной задачи
Найдите решение транспортной задачи, суть которой заключается в оптимальной организации транспортных перевозок штучного товара со складов в магазины (Таблица 28).
Таблица 28
Исходные данные транспортной задачи (транспортная матрица)
| Тарифы, руб./шт. | 1-й магазин | 2-й магазин | 3-й магазин | Запасы, шт. |
| 1-й склад | 2 | 9 | 7 | 25 |
| 2-й склад | 1 | 0 | 5 | 50 |
| 3-й склад | 5 | 4 | 100 | 35 |
| 4-й склад | 2 | 3 | 6 | 75 |
| Потребности, шт. | 45 | 90 | 50 |
2.1. Построение модели
Построим математическую модель для данной транспортной задачи.
1 шаг. Определение переменных
Обозначим через ![]() [шт.] количество штучного товара, которые будут перевезены с i-го склада (
[шт.] количество штучного товара, которые будут перевезены с i-го склада (![]() ) в j-тый магазин (
) в j-тый магазин (![]() ).
).
2 шаг. Проверка сбалансированности задачи
Общее количество товара, необходимое для удовлетворения спроса равно: 45+90+50=185 и доступно: 25+50+35+75=185, следовательно, задача сбалансирована.
3 шаг. Задание целевой функции
Формальная ЦФ, то есть суммарные затраты на все возможные перевозки товара, учитываемые в модели, задается выражением (12).
| ( 12) |
4 шаг. Задание ограничений
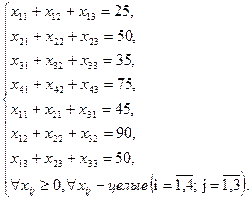 . . | (13) |
Так как объёмы перевозки товара не могут принимать отрицательные значения и должны быть целыми числами, то появляются условия неотрицательности и целостности:
| (14) |
- Напоминаем, что символ ![]() называется квантором всеобщности (читается «для любого»).
называется квантором всеобщности (читается «для любого»).
Таким образом, математическая модель задачи представлена в виде: определить объем ![]() , обеспечивающий минимальное значение функции:
, обеспечивающий минимальное значение функции:
при наличии ограничений:
| ( 15) |
2.2. Нахождение решения транспортной задачи в Microsoft Excel
Задание 6
Найдите оптимальный план перевозок, используя MicrosoftExcel, для этого выполните следующие действия:
1. Запустите приложение MicrosoftExcel.
2. Создайте экранную форму для ввода условия задачи (Рис. 13).
3. Введите исходные данные (Таблица 28) в экранную форму (Рис. 14).
4. Проверьте выполнение условия баланса, для этого:
· в ячейку G10 введите формулу СУММ(C10:F10), ав ячейку H9 введите формулу СУММ(H3:H6) ;
· если суммы равны, то в ячейке H10 напишите БАЛАНС (Рис. 15).
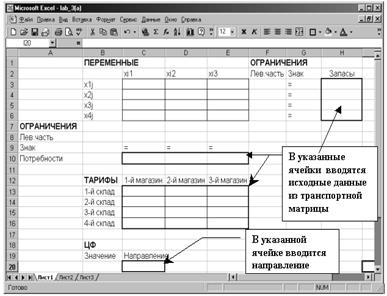
Рис. 13. Экранная форма транспортной задачи