Реферат: Тройные и кратные интегралы
Если, в частности, ![]() то интеграл выражает объём V области
то интеграл выражает объём V области ![]()
![]()
Вычисление тройного интеграла в цилиндрических координатах приводится к интегрированиям по r, по ![]() и по z на основании тех же принципов, что и в случае декартовых координат. В частности, если областью интегрирования служит внутренность цилиндра
и по z на основании тех же принципов, что и в случае декартовых координат. В частности, если областью интегрирования служит внутренность цилиндра ![]() то пределы трехкратного интеграла постоянны и не меняются при перемене порядка интегрирования:
то пределы трехкратного интеграла постоянны и не меняются при перемене порядка интегрирования:

3. Сферические координаты.
Отнесём теперь область интегрирования ![]() к системе сферических координат
к системе сферических координат ![]() . В этой системе координат положение точки M в пространстве определяется её расстоянием r от начала координат (длина радиуса-вектора точки), углом
. В этой системе координат положение точки M в пространстве определяется её расстоянием r от начала координат (длина радиуса-вектора точки), углом ![]() между радиусом-вектором точки и осью Oz и углом
между радиусом-вектором точки и осью Oz и углом ![]() между проекцией радиуса вектора точки на плоскость Oxy и осью Ox (рис. 6). При этом
между проекцией радиуса вектора точки на плоскость Oxy и осью Ox (рис. 6). При этом ![]() может изменятся то 0 до
может изменятся то 0 до![]() а
а ![]() - от 0 до
- от 0 до ![]() .
.
 |
Рис.6
Связь между сферическими и декартовыми координатами легко устанавливается. Из рис.6 имеем

Отсюда
![]() (**)
(**)
Разобьем область ![]() на частичные области
на частичные области ![]() , тремя системами координатных поверхностей:
, тремя системами координатных поверхностей: ![]() которыми будут
которыми будут
 |
соответственно сферы с центром в начале координат, полуплоскости, проходящие, через ось О z , и конусы с вершиной в начале координат и с осями, совпадающими с одной из полуосей О z . Частичными областями ![]() служат “шестигранники” (рис. 7). Отбросив бесконечно малые высших порядков, будем рассматривать шестигранник MN как прямоугольный параллелепипед с измерениями, равными:
служат “шестигранники” (рис. 7). Отбросив бесконечно малые высших порядков, будем рассматривать шестигранник MN как прямоугольный параллелепипед с измерениями, равными: ![]() по направлению полярного радиуса,
по направлению полярного радиуса, ![]() по направлению меридиана,
по направлению меридиана, ![]() по направлению параллели. Для элемента объема мы получимтогда выражение
по направлению параллели. Для элемента объема мы получимтогда выражение
![]()
Заменив в тройном интеграле ![]() по формулам (**) и взявэлемент объема равным полученному выражению, будемиметь
по формулам (**) и взявэлемент объема равным полученному выражению, будемиметь
![]()
Особенно удобно применение сферических координат в случае, когда область интегрирование ![]() - шар с центром в начале координат или шаровое кольцо.Например, в последнем случае, если радиус внутреннего шара
- шар с центром в начале координат или шаровое кольцо.Например, в последнем случае, если радиус внутреннего шара ![]() , а внешнего
, а внешнего ![]() , пределы интегрирования следует расставить так:
, пределы интегрирования следует расставить так:

Если ![]() - шар, то нужно положить
- шар, то нужно положить ![]()
A) Пример.
Вычислим объем шара радиуса R. В этом случае подынтегральную функцию надо взять равной 1, и мы получим
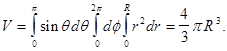
Применение тройных интегралов.
Для вычисления координат центра тяжести тела нужны статические моменты относительно координатных плоскостей Оху, Ох z , Оу z ; обозначим их соответственно ![]() Повторяя рассуждения получим следующие формулы для координат
Повторяя рассуждения получим следующие формулы для координат ![]() центра тяжести неоднородного тела, плотность которого задается функцией
центра тяжести неоднородного тела, плотность которого задается функцией ![]() занимающего область
занимающего область ![]() :
:
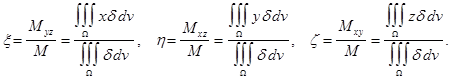
Если тело однородно, т. е. ![]() , то формулы упрощаются:
, то формулы упрощаются:
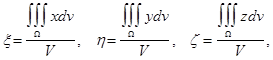
где V- объём тела.
Пример. Найдем центр тяжести однородного полушара ![]() :
:
![]()
Две координаты центра тяжести ![]() равны нулю, ибо полушар симметричен относительно оси О z (тело вращения с осью О z) .
равны нулю, ибо полушар симметричен относительно оси О z (тело вращения с осью О z) .
Интеграл ![]() удобно вычислить, перейдя к сферическимкоординатам:
удобно вычислить, перейдя к сферическимкоординатам:
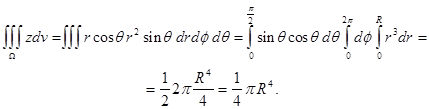
Так как объём полушара равен ![]() то
то
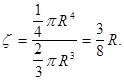
Перейдём к вычислению моментов инерции тела относительно координатных осей. Так как квадраты расстояний от точки P(x, y, z) до осей Ox, Oy, Oz соответственно равны ![]() то полагая для простоты
то полагая для простоты ![]() получим следующие формулы :
получим следующие формулы :
![]()
Аналогично плоскому случаю интегралы
![]()
называются центробежными моментами инерции.
Для полярного момента инерции формула имеет вид
![]()
Если тело неоднородное, то в каждой формуле под знаком интеграла будет находиться дополнительный множитель ![]() - плотность тела в точке P.
- плотность тела в точке P.
Пример. Вычислим полярный момент инерции однородного шара радиуса R. В этом случае очень удобно перейти к сферическим координатам. Будем иметь
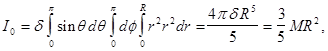
где ̗ масса шара.
Так как для сферы моменты инерции относительно осей координат, очевидно, равны между собой, то, учитывая, что ![]() получим
получим
![]()
Моменты инерции тела относительно оси играют важную роль при вычислении кинетической энергии тела при его вращении около соответствующей оси. Пусть тело ![]() вращается околооси Оzс постоянной угловой скоростью
вращается околооси Оzс постоянной угловой скоростью ![]() . Найдем кинетическую энергию
. Найдем кинетическую энергию ![]() тела. Как известно, кинетическая энергия точки измеряется величиной
тела. Как известно, кинетическая энергия точки измеряется величиной ![]() , где т - масса точки, а
, где т - масса точки, а ![]() - величина ее скорости. Кинетическая энергия системы точек определяется как сумма кинетических энергий отдельных точек, а кинетическая энергия тела - как сумма кинетических энергий всех частей, на которые оно разбито. Это обстоятельство позволяет применить для вычисления .кинетической энергии интеграл.
- величина ее скорости. Кинетическая энергия системы точек определяется как сумма кинетических энергий отдельных точек, а кинетическая энергия тела - как сумма кинетических энергий всех частей, на которые оно разбито. Это обстоятельство позволяет применить для вычисления .кинетической энергии интеграл.
Возьмем какую-нибудь окрестность ![]() точки Р(х, у, z ) тела
точки Р(х, у, z ) тела ![]() . Величина линейной скорости
. Величина линейной скорости ![]() точки Р при вращении около оси О z равна
точки Р при вращении около оси О z равна ![]() и значит, кинетическая энергия части
и значит, кинетическая энергия части ![]() тела
тела ![]() выразится так :
выразится так :
![]()
где ![]() - плотность тела в точке Р. Для кинетической энергии всего тела
- плотность тела в точке Р. Для кинетической энергии всего тела ![]() получаем
получаем
![]()