Тепер повинно бути очевидне, що сферична поверхня Фермі може бути виявлена в металі тільки через випадкові обставини. Набагато типовіша ситуація, коли магнітне поле BZ примушує електрони з енергією Фермі рухатися в до - просторі навколо поверхні Фермі по траєкторії, уздовж якої ефективна маса безперервно змінюється_. Тоді швидкість, з якою хвилевий вектор міняється з часом, непостійна; це ясно вже з того, що магнітна сила, що діє на електрон, рівна ћ(dkdt)і також рана –e(v´B.В результаті швидкість руху електрона по орбіті в реальному просторі не постійна.

У експериментах по циклотронному резонансу використовується поглинання електромагнітної енергії на радіочастотіw, коли магнітна індукція B підібрана таким чином, що w=_c . Тоді використання різних комбінацій і B дозволяє (в принципі) отримати інформацію щодо тензора ефективної маси для електрона з енергією Фермі. Фактична теорія циклотронного резонансу набагато складніша як для напівпровідників, так і для металів.

Для напівпровідникового матеріалу, в якому щільність вільних електронів мала, експерименти по циклотронному резонансу можуть бути виконані з електромагнітними хвилями, проникаючими в тверде тіло. Трудність, які при цьому виникають, пов'язані з топологією поверхонь постійної енергії і з гібридними плазмовими резонансами, у тому випадку, коли концентрація вільних електронів не дуже мала.

Частоти, використовувані для дослідження циклотронного резонансу в металі, завжди значно менше плазмової частоти (оскільки концентрація електронів в металі настільки велика, що і частота w_p стає великою). Для w<_p речова частина діелектричної проникності негативна. Відповідно до цього метал для таких частот непрозорий і глибина проникнення d (товщина скин-слоя) значно менше товщини зразка. В цьому випадку від середньої довжини вільного пробігу електрона l залежить, чим визначатимуться електричні характеристики поверхні для електромагнітних хвиль радіодіапазону: нормальним скін-ефектом або аномальним скін-ефектом. Перший випадок здійснюється при <d, а другий приl>d.

У останньому випадку можна порушити циклотронний рух, комбінуючи дію постійної магнітної індукції (наприклад, BZ) і високочастотного електромагнітного поля при цьому використовується геометрія, запропонована Азбелем і Канером мал.2. Названі автори вказали, що якщо постійна магнітна індукція BZ лежить в площині поверхні, то циклотронний рух повинен відбуватися в площині, що перетинає поверхню. Деякі циклотронні орбіти при цьому досягають області високочастотного скін-шару, орбітам, наближаючись до поверхні, можуть випробовувати дію високочастотного поля з кутовою частотою w і циклотронною частотою w_с. Таким чином, поверхневий імпеданс кристала по відношенню до високочастотного випромінювання є функцією величини магнітної індукції.

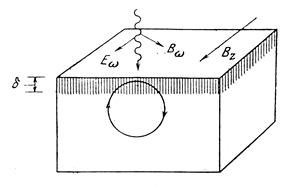
Мал.2. Геометрія Азбеля-Канера для спостереження циклотронного резонансу в металевому кристалі

Заштрихований скін-шар, що має глибину d для високочастотного випромінювання з частотою w Показана одна з можливих орбіт, що проходять через поверхневий шар. Така орбіта може відповідати циклотронному руху, що виникає під дією магнітної індукції Bz, прикладеної в площині поверхні. Спостереження резонансу Азбеля-Канера повинне проводитися на металевому монокристалі високої частоти і досконалості, Високої частоти і досконалості, одна грань якої [наприклад, (100) або (111)] оброблена з особливою ретельністю, щоб при низьких температурах середній час вільного пробігу (а отже, середня довжина вільного пробігу) був великий як в об'ємі кристала, так і в скін-шарі. Енергія високочастотного поля може бути пов'язана з енергією кругового руху електронів за умови l>d. Якщо при цьому також w_сm t»1, то може спостерігатися гострий циклотронний резонанс, коли частота рівна або кратна _с.

Для успішного спостереження резонансних явищ слід працювати з чистим досконалим монокристалом при низьких температурах, щоб середня довжина вільного пробігу була велика в порівнянні з розміром циклотронної орбіти. Поверхня, на яку падає високочастотне випромінювання, повинна бути хорошої якості, щоб значення l в при поверхневому шарі було таким же, як в об'ємі. У цих умовах значення l буде великим в порівнянні з товщиною скін-шару d і рухомий по колу електрон взаємодіятиме з високочастотним полем тільки протягом малої частки свого періоду звернення. Азбель і Канер вказали, що при l>d і (w_cm t)»1 взаємодія між високочастотним полем і циклотронним рухом може бути забезпечене як при =_з , так і при значенні, достатньо малому кратному _с. Хай Bc - магнітна індукція, при якій _{= с.} Для магнітної індукції, складовій цілу частку від Bc, інтервал між двома послідовними попаданнями даного електрона в поверхневий шар рівний декільком періоду високочастотного поля. Проте і в цьому випадку високочастотне поле зможе повторити свою дію на електрон в той момент, коли він знову опиниться біля поверхні.

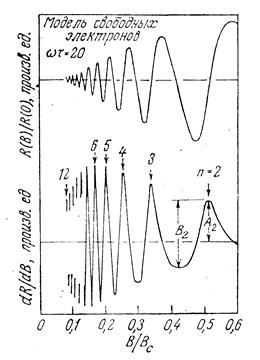
Мал.3. Залежність поверхневого опору (речовій частині поверхневого імпедансу) для вільного електронного газу в металі при частоті високочастотного поля w від індукції B (верхня крива)

По осі абсцис отложна нормована величина B/Bc, де

Bc=индукцияwme—,

для якої w і циклотронна частота співпадають. Ця крива може бути розрахована по формулі моделі Азбеля-Канера.

Азбель і Канер встановили, що залежність комплексного поверхневого імпедансу від магнітної індукції визначається виразом

Z(B)=Z[1–exp(–2p/wt_m )exp(–2piw_c w)]^{1 / 3} ,

де магнітна індукція входить у величину w_c . Осцилююча поведінка речової частини цього імпедансу (поверхневого опору) показана на рис.3. Там же показаний хід похідної (dRdB) – величини, яку можна вимірювати безпосередньо в експерименті.

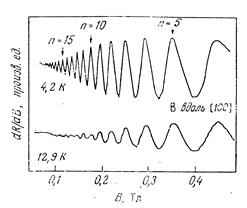
Мал.4. Результати експериментального спостереження резонансу Азбеля-Канера в кристалі чистої міді при двох температурах

Крива для вищої температури згладжена із-за збільшеного теплового розсіяння рухомих по циклотронній орбіт електронів. Поверхнею кристала є площина (110), магнітне поле, направлене уподовж [100], лежить в цій площині. Спостерігається резонанс для електронів, рухомих по екстремальній «поясній орбіті», що охоплює основний об'єм поверхні Фермі.(див. Мал.5).

На Мал.4. приведені для прикладу результати експериментального спостереження резонансу Азбеля-Канера на дуже чистому зразку міді при низьких температурах. Відмінність два кривих показує, як важливо, щоб розсіяння електронів було зведене до мінімуму. Криву, зняту при 4,2К, можна безпосередньо порівняти з прогнозами теорії Азбеля-Канера і визначити з неї розмір орбіти для електронів з енергією Фермі в міді. Для такої орієнтації полів, при якій були отримані дані на рис.3, важлива електронна «поясна» орбіта (bellyorbit), коли електрони рухаються в до - просторі майже по круговій траєкторії навколо основного обхвату поверхні Фермі, показаної на мал.4.

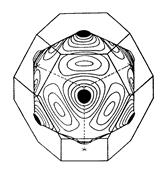
Мал.4. Поверхня Фермі для міді.

Поверхня Фермі в цьому металі формується електронами, розташованими в заповненій наполовину 4s-зоне.

Поясна орбіта є екстремальною; Вона максимізувала циклотронний період; так само «шеечная орбіта» навколо шийки, показаної біля кордону зони на рис.4. і рис.5., екстремальна в тому сенсі, що вона мінімізує циклотронний період в порівнянні з сусідніми орбітами.

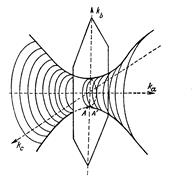
Мал.5. Частина ферми - поверхні міді, показана в представленні зон, що повторюються.

Для енергетичних перебувань на межі зони ефективна маса позитивна у напрямі kb і kc, але негативна в напрямі, перпендикулярному площині зонної межі. Частина ферми - поверхні, що має форму такого типу, відома в літературі під назвою «шийки». У магнітному полі електрон можна змусити процесувати навколо такої «шеечной орбіти» постійної енергії.

Особлива важливість екстремальних орбіт пов'язана з тим, що електрони, що процесують по орбітах, лежачих на несферичній поверхні Фермі, володіють в даному магнітному полі безліччю періодів. Проте внески електронів з не екстремальних орбіт взаємно компенсуються із-за відмінності фаз. Основний внесок дає екстремальна область, в якій перша похідна періоду після компоненту до, направленою уздовж магнітного поля, звертається в нуль. Ця область відповідальна за значний сигнал, що знаходиться у фазі.

Висновок