Реферат: Учение о параллельности. Открытие неевклидовой геометрии
- Существует прямоугольник (хотя бы один ), то есть четырёхугольник, у которого все углы прямые.
- Существуют подобные, но не равные треугольники (аксиома Валлиса , 1693).
- Любую фигуру можно пропорционально увеличить.
- Существует треугольник сколь угодно большой площади.
- Прямая, проходящая через точку внутри угла, пересекает по крайней мере одну его сторону (аксиома Лоренца ,1791).
- Через каждую точку внутри острого угла всегда можно провести прямую, пересекающую обе его стороны.
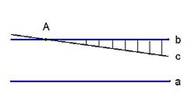
- Если две прямые в одну сторону расходятся, то в другую – сближаются.
- Сближающиеся прямые рано или поздно пересекутся.
- Вариант: перпендикуляр и наклонная к одной и той же прямой непременно пересекаются (аксиома Лежандра).
- Точки, равноудалённые от данной прямой (по одну её сторону), образуют прямую,
- Если две прямые начали сближаться, то невозможно, чтобы они затем начали (в ту же сторону, без пересечения) расходиться (аксиома Роберта Симсона , 1756).
- Сумма углов одинакова у всех треугольников.
- Существует треугольник, сумма углов которого равна двум прямым.
- Две прямые, параллельные третьей, параллельны и друг другу (аксиома Остроградского , 1855).
- Прямая, пересекающая одну из параллельных прямых, непременно пересечёт и другую.
- Через любые три точки можно провести либо прямую, либо окружность.
- Вариант: для всякого невырожденного треугольника существует описанная окружность (аксиома Фаркаша Бойяи ).
- Справедлива теорема Пифагора.
Эквивалентность их означает, что все они могут быть доказаны, если принять V постулат, и наоборот, заменив V постулат на любое из этих утверждений, мы сможем доказать исходный V постулат как теорему.
Если вместо V постулата допустить, что для пары точка–прямая V постулат неверен, то полученная система аксиом будет описывать геометрию Лобачевского. Понятно, что в геометрии Лобачевского все вышеперечисленные эквивалентные утверждения неверны.
Система аксиом сферической геометрии требует изменения также и других аксиом Евклида..
Пятый постулат резко выделяется среди других, вполне очевидных, он больше похож на сложную, неочевидную теорему. Евклид, вероятно, сознавал это, и поэтому первые 28 предложений в «Началах» доказываются без его помощи.
«Евклиду безусловно должны были быть известны различные формы постулата о параллельных». Почему же он выбрал приведенную, сложную и громоздкую? Историки высказывали различные предположения о причинах такого выбора. В.П. Смилга полагал, что Евклид такой формулировкой указывал на то, что данная часть теории является незавершённой. М. Клайн обращает внимание на то, что пятый постулат Евклида имеет локальный характер, то есть описывает событие на ограниченном участке плоскости, в то время как, например, аксиома Прокла утверждает факт параллельности, который требует рассмотрения всей бесконечной прямой. Надо пояснить, что античные математики избегали использовать актуальную бесконечность; например, второй постулат Евклида утверждает не бесконечность прямой, а всего лишь то, что «прямую можно непрерывно продолжать». С точки зрения античных математиков, вышеприведенные эквиваленты постулата о параллельных могли казаться неприемлемыми: они либо ссылаются на актуальную бесконечность или (ещё не введенное) понятие измерения, либо тоже не слишком очевидны.
Абсолютная геометрии.
Если из списка аксиом исключить V постулат, то полученная система аксиом будет описывать так называемую абсолютную геометрию. В частности, первые 28 теорем «Начал» Евклида доказываются без использования V постулата и поэтому относятся к абсолютной геометрии. Для дальнейшего отметим две теоремы абсолютной геометрии:
- Параллельные прямые существуют; это следует из теорем 27 и 28 «Начал» Евклида.
- При продолжении двух прямых от точки их пересечения расстояние между ними неограниченно возрастает.
Попытки доказательства
Математики с давних времён пытались «улучшить Евклида» – либо исключить пятый постулат из числа исходных утверждений, то есть доказать его, опираясь на остальные постулаты и аксиомы, либо заменить его другим, столь же очевидным, как другие постулаты. Надежду на достижимость этого результата поддерживало то, что IV постулат Евклида (все прямые углы равны ) действительно оказался лишним – он был строго доказан как теорема и исключён из перечня аксиом.
За два тысячелетия было предложено много доказательств пятого постулата, но в каждом из них рано или поздно обнаруживался порочный круг: оказывалось, что среди явных или неявных посылок содержится утверждение, которое не удаётся доказать без использования того же пятого постулата.