Реферат: Уравнения Больцмана, Лиувилля, Боголюбова

Безразмерная форма уравнений Боголюбова. Факторизация и корреляционные функции. Свободно-молекулярное течение

Рассмотрим некоторые приближенные методы интегрирования системы уравнений Боголюбова. Эти методы основаны на том, что в двух случаях - весьма разреженного газа и при слабом взаимодействии между частицами газа - влияние одной частицы на состояние других частиц должно становиться слабым, и можно сделать пробное допущение о том, что в нулевом приближении n-частичная функция распределения факторизуется, т. е. представляется в виде произведения одночастичных функций

. (15)

Отклонение точной n-частичной функции от факторизованного нулевого приближения принято характеризовать с помощью так называемых корреляционных функций Gn (x1, ..., хп, t), которые находятся по следующей схеме.

Для двухчастичной функции имеем

F2(0) (х1, х2, t) = F1 (х1, t) F1 (х2, t), (16)

F2 (x1, x2, t) = F2(0) (x1, x2, t) + G2 (x1, x2, t). (17)

Для трехчастичной функции -

F3(0) (х1, х2,x3, t) = F1 (х1, t) F1 (х2, t) F1 (х3, t), (18)

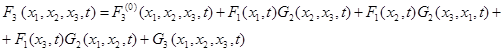(19)

и т. д.

Сформулируем теперь количественно условие разреженности газа и условие слабости взаимодействия. Пусть r0 — радиус действия межмолекулярных сил и U0 — характерная величина потенциальной энергии взаимодействия. Случай разреженного газа осуществляется, если r0 много меньше среднего расстояния между частицами ω1/3, и, следовательно, в этом случае малым параметром задачи является величина . Случай слабого взаимодействия реализуется, если потенциальная энергия мала по сравнению с кинетической энергией ~ Т. Следовательно, в этом случае малым параметром задачи является величина β= U0/T.

Допустим, что в обоих случаях корреляции между координатами и скоростями частиц являются слабыми и корреляционные функции Gn (x1, ..., хп, t) малыми по параметрам а или β соответственно.

Для того чтобы построить методы решения системы уравнений Боголюбова в этих предположениях, запишем систему (7) в более детализированном виде

(20)

выделив в операторе слагаемые, содержащие и не содержащие потенциал взаимодействия

(21)

( 22)

(23)

Перейдем в уравнениях (20) безразмерным переменным, выбрав в качестве единицы длины r0, скорости , ускорения и времени . Для простоты мы не будем вводить новые обозначения для безразмерных переменных и сделаем в уравнениях (20) замены

,

(24)

Кроме того, учитывая условие нормировки (19) для функци Fn(x1, ..., хN, t), из которого видно, что Fn имеет размерность , введем безразмерную функцию распределения с помощью замены

(25)

Тогда уравнения Боголюбова (20) при запишутся в виде

(26)

Заметим, что, предполагая факторизацию функций Fn в нулевом приближении,

Fn(0) = F1 (х1, t) F1 (х2, t)…F1(xn,t), мы получим для одной и той же функции F1 (xi, t) N уравнений. Ясно, что необходимым условием допустимости факторизации является совместность этих уравнений нулевого приближения.

Убедимся, что случай разреженного газа () приводит в нулевом приближении к несамосогласованной системе. Действительно, система уравнений (26) в нулевом приближении выглядит следующим образом: