Реферат: Уравнения и способы их решения

Эта формула известная как формула Кардано .

Тригонометрическое решение

подстановкой приводится к "неполному" виду

, , . (14)

Корни , , "неполного" кубичного уравнения (14) равны

, ,

где

, ,

.

Пусть "неполное" кубичное уравнение (14) действительно.

а) Если ("неприводимый" случай), то и

,

,

где

.

(b) Если , , то

, ,

где

, .

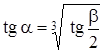
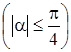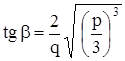
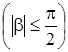(с) Если , , то

, ,

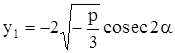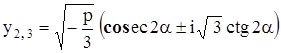где

, .

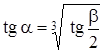
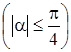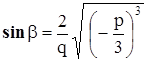
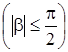Во всех случаях берется действительное значение кубичного корня.

Биквадратное уравнение

Алгебраическое уравнение четвертой степени.

,

где a, b, c – некоторые действительные числа, называется биквадратным уравнением . Заменой уравнение сводится к квадратному уравнению с последующим решением двух двучленных уравнений и ( и - корни соответствующего квадратного уравнения).

Если и , то биквадратное уравнение имеет четыре действительных корня:

, .

Если , [3] ), то биквадратное уравнение имеет два действительных корня и мнимых сопряженных корня:

.

Если и , то биквадратное уравнение имеет четыре чисто мнимых попарно сопряженных корня:

, .

Уравнения четвертой степени

Метод решения уравнений четвертой степени нашел в XVI в. Лудовико Феррари, ученик Джероламо Кардано. Он так и называется – метод Феррари .

Как и при решении кубического и квадратного уравнений, в уравнении четвертой степени

можно избавиться от члена подстановкой . Поэтому будем считать, что коэффициент при кубе неизвестного равен нулю:

.

Идея Феррари состояла в том, чтобы представить уравнение в виде , где левая часть – квадрат выражения , а правая часть – квадрат линейного уравнения от , коэффициенты которого зависят от . После этого останется решить два квадратных уравнения: и . Конечно, такое представление возможно только при специальном выборе параметра . Удобно взять в виде , тогда уравнение перепишется так:

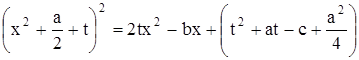. (15)

Правая часть этого уравнения – квадратный трехчлен от . Полным квадратом он будет тогда, когда его дискриминант равен нулю, т.е.

, или

.

Это уравнение называется резольвентным (т.е. "разрешающим"). Относительно оно кубическое, и формула Кардано позволяет найти какой-нибудь его корень . При правая часть уравнения (15) принимает вид

,

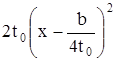а само уравнение сводится к двум квадратным:

.

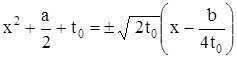Их корни и дают все решения исходного уравнения.

Решим для примера уравнение

.

Здесь удобнее будет воспользоваться не готовыми формулами, а самой идеей решения. Перепишем уравнение в виде