Реферат: Уточнение простой теории МО ЛКАО. Базисная АО. Эффективный заряд-показатель экспоненты
для расчёта числовых значений специальных несобственных интегралов вида:
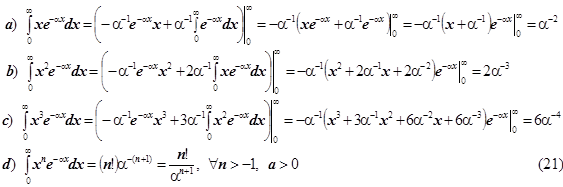
Расчёт энергетические уровни МО
(с варьированием показателя экспоненты базисных водородоподобных АО).
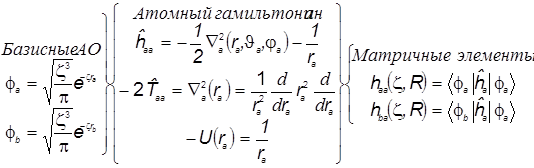 . (22 Напомним, что в шаровых координатах лапласиан имеет вид
. (22 Напомним, что в шаровых координатах лапласиан имеет вид
![]() . ( 23 )
. ( 23 )
Поскольку выбранные нами базисные s-АО не зависят от угловых переменных, то и результат действия на них угловой части лапласиана, составляющей оператор Лежандра, нулевой. Поэтому имеет смысл в выкладках оставить лишь радиальную часть лапласиана, а соответственно, символ частного дифференцирования следует заменить символом полного дифференцирования по единственной оставшейся переменной r .
Вычисление матричных элементов одноцентрового
(атомного) гамильтониана
1) Диагональные матричные элементы haa = hbb
![]() . ( 24 )
. ( 24 )
Нижний индекс в данном пункте расчёта удобно опустить.
Слагаемое 1 (порождено потенциальным слагаемым атомного гамильтониана):
![]() . ( 25 )
. ( 25 )
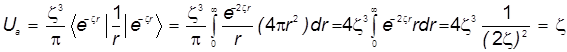 ; ( 26)
; ( 26)
![]() . (27)
. (27)
Слагаемое 2 (порождено кинетическим слагаемым атомного гамильтониана):
Это слагаемое рассчитывается по формуле:
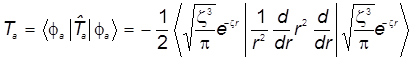 . (28)
. (28)
а) Заменим дифференциальные операции более простыми выражениями. Для этого рассмотрим преобразуем волновую функцию, следуя операторному уравнению![]() :
:
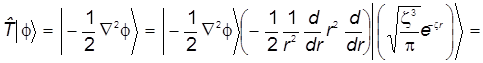
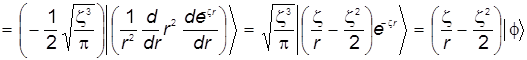 . (29)
. (29)
Из последней цепочки равенств следует координатное выражение атомного оператора кинетической энергии. Опуская в ней промежуточные и оставляя лишь начальное и конечное выражения, приходим к привычной форме операторного уравнения:
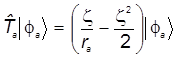 . (30)
. (30)
б) Умножая последнее равенство слева на бра-вектор, получаем искомые кинетические слагаемые и диагонального и недиагонального матричных элементов атомного гамильтониана:
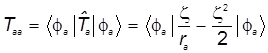 , (31)
, (31)
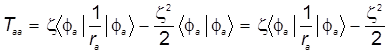 . (32)
. (32)
Учитывая нормировку АО ![]() , а также принимая во внимание равенство
, а также принимая во внимание равенство
![]() , получаем:
, получаем: ![]() . (33)
. (33)
Диагональный матричный элемент одноцентрового гамильтониана получается суммированием потенциального и кинетического слагаемых. Он не зависит от межъядерного расстояния:
![]() . ( 34)
. ( 34)
2) Недиагональные матричные элементы hab = hba