Реферат: В поисках определения термина «информация»
Таким образом, если имеется несколько форм представления одного содержания информации, то вышепреведенная трактовка категории «форма-содержание» как перехода одного в другое — неверна.
Обратимся к задаче, решаемой формулой Шеннона: есть содержание, которое оптимальным образом необходимо передать из одной точки в другую. Ключевое требование в этой задаче — оптимально, следовательно, существует несколько способов, т.е. форм передачи.
Из вышесказанного следует, что в принципе форма и содержание различны, но связанны между собой "на уровне способа выражения и существования содержания". [Верещагина]
Более того, раз это так, для человеческого восприятия существует несколько форм одного содержания.
Говоря о множественности форм одного содержания следует иметь ввиду, что при доказательстве множественности форм имелась ввиду субъективная информация; та информация, которая используется человеком. Но тем не менее, не смотря на эту оговорку суть доказательства, на взгляд автора, не меняется.
Формула количества информации
Формула Шеннона, измеряющая количество информации (1) выглядит так:
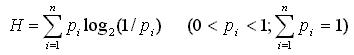
где H — символ количества информации, воплощенной в некоторой системе, i — индекс состояний ситсемы, n — число состояний, p i — вероятность состояния i .
Формула предназначена для измерения количества информации в системах, которым присуще конечное количество дискретных состояний, различающихся по распространенности внутри соответствующих систем. Доказано, что формула Шеннона выражает единственно возможную меру количества информации с системах указанного в ней типа (с точностью до постоянного множителя, который служит для выбора единицы информации). [Файнстейн] сс.10-14
Величина H в формуле Шеннона представляет собой математическое ожидание информации, воплощенной в некоторой системе, имеющей различный состояния i . Единичная информация, воплощеная в состоянии i , определяется по формуле:
I i = log 2 (1/ p i ) (2)
Если система имеет только одно состояние ( n = 1), то для него p i = 1, I i = 0, соответственно M = 0. Если n >= 2, то все вероятности p < 1, все I i > 0, соответственно, H > 0
Вклад каждого из состояний в общую (среднюю) информацию, содержащуюся в ней, определяется величиной
M i = p i I i (3)
Было бы неверно полагать, что этот вклад тем больше, чем больше I i , т.е. чем меньше p i .
M i max достигается при p i = e -1 ~ 0.37 ( M i max = 0.5307); M i убывает вплоть до нуля как при уменьшении, так и при увеличении вероятности по отношению к этому значению.
С учетом (3) формула (1) выглядит так:
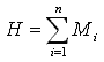
Общее количество информации в системе есть сумма ее величин, воплощенных в состояниях системы.
Некоторые выводы
Подведем нашим рассуждениям небольшой итог.
Информация как таковая существует независимо от нас, как одна из трех субстанций Универсума. В этом понимании информация является мерой организации, присущей материальным объектам.
Говоря об информации как таковой, мы имеем ввиду количественный смысл только одной из ее составляющих: объективной либо субъективной.
Объективная информация — часть субстанции, неподвластная нашим намерениям; она существует независимо от нас и нашего представления о ней. Говорить, таким образом, о конкретном содержании (качественном смысле) объективной информации неверно.
Субъективная информация — часть субстанции, подвластная нам: мы можем получать ее из окружающих нас объектов или систем. Субъективной информации не существует без участия субъекта: она появляется в момент получения ее субъектом и в этот же момент аннигилирует (перестает существовать), переходя в сведения.
Количество получаемой субъективной информации тесно связано с количеством знаний у субъекта: дополнительные знания дают возможность получения дополнительной субъективной информации, не доступной другим субъектам, у которых отсутствуют эти знания. Говорить, таким образом, о качественном смысле (конкретном содержании) субъективной информации в общем виде (применительно к множеству субъектов) неверно, в силу того, что восприятие субъективной информации индивидуально для каждого субъекта.
Форма и содержание: сущности, обязательно присутствующие вместе, но не зависящие друг от друга настолько, насколько это возможно. Принципиально возможна количественная оценка различных форм, без привязки к содержанию, следовательно задача по поиску оптимальной формы для заданного содержания теоритически выполнима.
Количество информации в системе может быть увеличено путем равномерного перераспределения вероятностей существующих состояний, без введения новых.
Список литературы
Вальтух К.К. Информационная теория стоимости в неравновесных системах. "Янус-К" 2001