Реферат: Варианты алгоритма возведения в степень повышение точности и ускорение
fsubp //st(0)=dx
//Подсчет по схеме Горнера. Мне казалось, что можно сделать это быстрее,
//пустив параллельно несколько цепочек вычислений, но пока это не удалось сделать.
fld qword ptr coeffspow[4*eax]
fmul st,st(1)
fld qword ptr coeffspow[4*eax+8]
faddp
fmul st,st(1)
fld qword ptr coeffspow[4*eax+16]
faddp
fmul st,st(1)
fld qword ptr coeffspow[4*eax+24]
faddp
fxch st(1)
fstp st //Освобождаем ненужный регистр
end;
ПРЕДУПРЕЖДЕНИЕ
Выполнение этого фрагмента изменяет содержимое регистра EAX.
Оценим погрешность приближения. Так как результат, получаемый как _Power(2,x) (функция _Power приведена в начале статьи), заведомо точнее, чем Exp2(x), то в качестве оченки примем относительное отклонение значения последней функции от значения первой: Epsilon=abs( Exp2(x) - _Power(2,x) ) / _Power(2,x). Разумеется, выражение имеет смысл, если _Power(2,x)<>0.
Если построить график относительной погрешности, становится видно, что в пределах каждого из 1998 отрезков он имеет форму кривой с одним максимумом, сходящей к нулю на концах отрезка. При этом пределы колебаний величины погрешности остаются постоянными на всех отрезках, кроме нескольких последних – на них погрешность возрастает. Если не принимать во внимание эти отрезки, и ограничить область допустимых значений аргумента числом 990 (т.е. x<990), то для описания поведения относительной погрешности в зависимости от x достаточно показать ее график на двух последних допустимых для значений x отрезках:
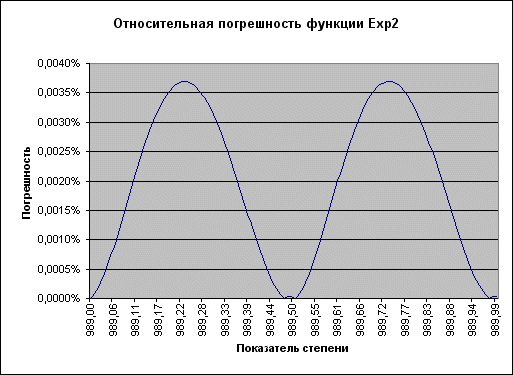
Рисунок 1. Максимальная погрешность приближения функции Exp2=2**x (при x менее 990) не превышает 0,004%.
|
СОВЕТ Мы отсекли отрезки, лежащие правее точки x=990. Следовательно, размер таблицы коэффициентов можно несколько сократить: индекс последнего элемента должен быть 990*2=1980, а не 1998. “Лишние” 19 последних строк таблицы можно просто удалить. Логично также изменить текст комментария в начале функции Exp2. |
Новый вариант функции возведения в степень
Изменим реализацию возведения в степень в соответствии с предложенной аппроксимацией для 2**x:
|
function New_Power(x,y:FLOATTYPE):FLOATTYPE; //abs(y*log2(x))<990 asm fld y К-во Просмотров: 424
Бесплатно скачать Реферат: Варианты алгоритма возведения в степень повышение точности и ускорение
|