Реферат: Варианты алгоритма возведения в степень повышение точности и ускорение
TEST AX, 256 or 16384 //0<= y*log2(x) ?
JZ @Reverse //Нет, случай со взятием обратного значения
ПРЕДУПРЕЖДЕНИЕ
Вдобавок в этом случае изменяется регистр EAX.
Результаты тестирования отражены на графиках:
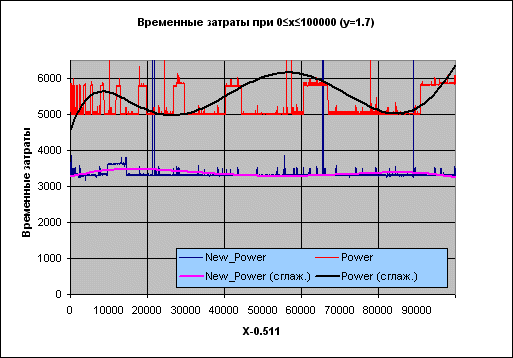
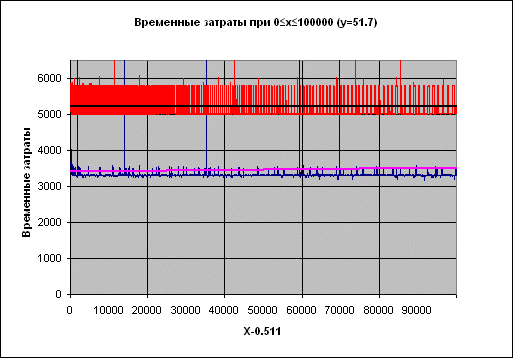
Рисунок 2. Временные затраты: New_Power – новая функция, Power – из состава RTL Borland Delphi.
Подпись X-0.511 на оси абсцисс отражает тот факт, что при проведении испытаний брались значения целые значения X, к которым затем прибавлялось число 0.511, чтобы гарантировать, что основание степени – число нецелое (т.е. чтобы рассматривать по возможности общий случай).
Черная линия поверх красного набора – сглаженные временные затраты функции Power, фиолетовая поверх синего – функции New_Power.
Замеры временных затрат производились с помощью инструкции RDTSC (процессоры начиная с Pentium):
|
function time:int64; //Вспомогательная функция для подсчета времени работы asm rdtsc end; |
и далее в коде
|
t:=time(); ... writeln(time()-t); |
RDTSC возвращает в регистровой паре EDX:EAX число тактов процессора, прошедших с момента последнего сброса (reset). Машинный код инструкции – 0Fh, 31h.
Относительная погрешность ведет себя на удивление стабильно, изменяясь в пределах от 0 до 0,0040%. Поэтому достаточно представительным множеством значений аргумента является, к примеру, промежуток (0, 1000).
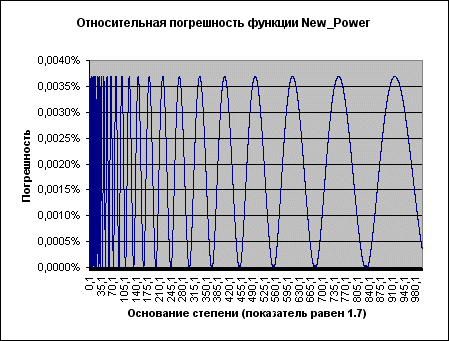
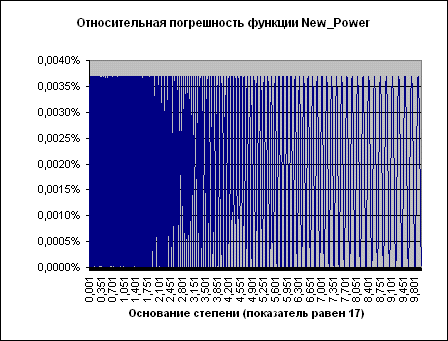
Рисунок 3.
Видно, что оцененная относительная погрешность (фактически - отклонение от значения, возвращаемого встроенной функцией) на самом деле не превосходит 0.004% !
В случае показателя степени 17 колебания становятся намного чаще, однако общая картина та же.
Аппроксимация функции log2x и “специализация” возведения в степень
Логарифмирование плохо поддается аппроксимации с помощью кубических сплайнов – точнее, мне удалось это сделать, причем с весьма высокой точностью, но лишь ценой проигрыша по времени в сравнении с использованием FYL2X. Однако здесь есть что предпринять и не прибегая к сплайнам.
Как известно, функция ln(1+x) при |x|<1 разлагается в ряд Тейлора следующим образом:
ln(1+x)=x-x2/(1*2)+x3/(1*2*3)+…+ xi/i!+…
Если абсолютная величина x достаточно мала, члены ряда, уже начиная с третьего, достаточно слабо сказываются на результате. Поэтому для значений x, достаточно близких к 1 (чтобы остаться в оговоренных выше рамках приемлемых погрешностей, x должен отстоять от 1 не больше чем на 0.01), вычисление log2(x)=ln(x)/ln(2)=ln(x)*log2(e)=ln(1+(x-1))*log2(e) можно заменить вычислением (t-t*t/2)*log2(e), где t=x-1.
Это позволяет построить еще один вариант функции возведения в степень для значений основания, близких к 1. В нем нет инструкции FYL2X, а вместо нее присутствует блок инструкций, помеченных символом “ * ” (знак “~” означает приближенное равенство):
|
К-во Просмотров: 423
Бесплатно скачать Реферат: Варианты алгоритма возведения в степень повышение точности и ускорение
|