Реферат: Визначення емпіричних закономірностей

Скоротимо обидва рівняння на -2 і зробимо такі перетворення:

Враховуючи, що , дістанемо:

(9)

Опустивши індекси перепишемо систему (9.9) так:

(10)

Одержана система рівнянь називається нормальною системою Гауса. Розв’язавши її знайдемо значення і .

; (11)

; (12)

в) Нехай функціональна залежність має такий вигляд: . Формула (9.6) в цьому випадку запишеться так:

.

Щоб знайти значення коефіцієнтів , і , при яких функція мінімальна, знаходимо часткові похідні по , і від і прирівнюємо їх до нуля. Розв’язання одержаної системи трьох рівнянь і дають нам значення , і , при яких буде мінімальним:

Прирівнявши ці похідні до нуля і зробивши відповідні перетворення, будемо мати:

(13)

Систему (9.13) запишемо без індексів:

(14)

Розв’язок цієї системи , і - це ті значення коефіцієнтів рівняння зв’язку другого степеня , при яких сума квадратів відхилень фактичних даних від вирівняних буде мінімальною.

, (15).

де

, (16)

, (17)

.

г) Аналогічно складається система нормальних рівнянь тоді коли зв’язок між ознаками близький до оберненого і досить добре виражається залежністю 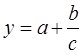. Система нормальних рівнянь для цього випадку буде такою: