Реферат: Визуализация в ГИС при наличии пространственных ограничений
где C=(x0 , y0 ) - центр дуги, вокруг которой вводится пространственная окрестность,
r - радиус дуги,
d -длина пространственной окрестности,
x, y - координаты рассматриваемого примитива,
A - точка, расположенная в начале дуги,
B - точка, расположенная в конце дуги,
D - точка, расположенная на одной оси с точкой ‘C’ со смещением
вправо, например (x0 +1, y0 ).
Определение факта попадания примитива в пространственную окрестность, заданную дугами окружностей, при разрезании примитивов аналогично пространственным ограничениям из окружностей.
4) ограничения, задаваемые произвольными многоугольниками:
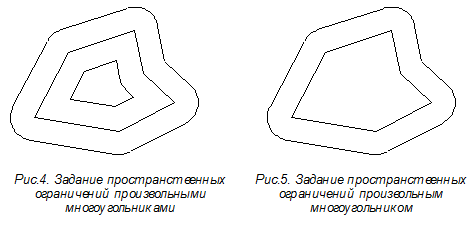
Как видно из рис.4-5 многоугольник, описывающий пространственную окрестность, не может быть получен простым масштабированием исходного контура (контура, описывающего заданный объект) по двум причинам:
a) для произвольного многоугольника, в общем случае, невозможно найти такую точку, которая была бы равноудалена от всех вершин этого многоугольника. Следовательно, нет такой точки, относительно которой операция масштабирования отодвинула бы стороны многоугольника, задающего пространственные ограничения, от сторон многоугольника-контура объекта на одинаковые расстояния.
b) стороны многоугольника, описывающего пространственную окрестность, как демонстрируют рис.4 и рис.5, ограничены дугами окружностей на внутренних углах, меньших ![]() .
.
Исходя из этих причин, предлагается следующий алгоритм, который учитывает все особенности преобразования контуров. Суть алгоритма заключается в следующем:
Из исходного множества вершин P (|P|=N) контура, описывающего заданный объект, строятся уравнения прямых (соответствующие формулы широко освещаются во всех печатных изданиях по машинной графике и аналитической геометрии, например, в [1-4]).
Согласно результатам, полученным в предыдущем пункте, строятся уравнения прямых многоугольника, задающего пространственные ограничения. Данные прямые смещены в направлении от контура объекта (см. случай, изображенный на рис. 5) и к контуру объекта (см. случай, изображенный на рис. 4). Уравнения прямых, параллельных ребрам многоугольного контура, можно построить по [4].
По формуле, аналогичной (1.б), определяются неравенства, ограничивающие отрезки полученного многоугольника в его углах.
Определяется множество V1 точек пересечения соседних отрезков и множество V2 точек пересечения отрезков и соответствующих окружностей, полученных из неравенств на шаге 3.
Последовательно обходя контур, из множеств V1 и V2 формируется искомое множество V вершин многоугольника, описывающего пространственную окрестность заданного объекта.
В итоге, любой примитив, попадающий в окрестность объекта, должен удовлетворять хотя бы одному из условий:
примитив попадает или пересекает многоугольник, составленный из вершин множества V;
координата примитива удовлетворяет одному из условий неравенств, полученных из неравенств на шаге 3.
Если примитив пересекает контур пространственной окрестности, то его необходимо разрезать в точках пересечения, пользуясь обобщенными на случай разрезаемого примитива алгоритмами разрезания произвольной прямой произвольным многоугольником. Данные алгоритмы описаны в [1] и [2], а более полный анализ приведен в [3]. Представим результаты анализа таких алгоритмов, приведенные в [3].
Таблица 1.
Разрезание отрезков прямой многоугольным окном
| Название метода | Окно | Элементарная операция | Сложность |
| Сазерленда (дихотомический вариант) | Прямоугольное |
Сравнение положения точки и контура (с кодированием) Вычисление середины отрезка | O(Log2 (размер отрезка)) |
| Сазерленда-Коэна | Прямоугольное и выпуклое |
Кодирование точки относительно контура К-во Просмотров: 511
Бесплатно скачать Реферат: Визуализация в ГИС при наличии пространственных ограничений
|