Реферат: Волновое сопротивление
При решении различного рода прикладных задач акустики, важное значение приобретают величины различных акустических сопротивлений — акустического, удельного акустического и механического.
Все эти сопротивления имеют активную и реактивную (управляемую гибкостью или массой)·составляющие.
Акустическое сопротивление
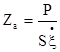 , (1)
, (1)
где Ρ — звуковое давление;
![]() — колебательная скорость в системе;
— колебательная скорость в системе;
S — площадь, для которой определяют сопротивление.
Акустическое сопротивление используют при исследовании вопросов распространения звуковых волн в звукопроводах переменного сечения с поперечными размерами меньше длины волны. В этом случае сопротивление остается постоянным, так как давление вдоль канала не изменяется, а колебательная скорость изменяется обратно пропорционально площади поперечного сечения.
Удельное акустическое сопротивление, называемое иногда также волновым, определяется отношением величины звукового давления в определенной точке среды к величине колебательной скорости в этой же точке:
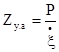 . (2)
. (2)
Удельное акустическое сопротивление безграничной среды определяется произведением плотности на величину скорости распространения звука в среде:
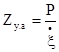 . (3)
. (3)
Таким образом, измерение удельного акустического сопротивления для безграничной однородной среды (практически это соответствует случаю, когда размеры образцов исследуемого материала значительно превышают длину звуковой волны) сводится κ измерению плотности среды и скорости распространения в ней звука.
Для малых размеров вещества по сравнению с длиной волны, неоднородных, имеющих сложную форму, удельное акустическое сопротивление по формуле (3) определить нельзя, кроме того, оно имеет комплексный характер, что обусловлено наличием угла сдвига фаз между звуковым давлением и колебательной скоростью.
Механическое сопротивление ![]() численно равно отношению силы F, действующей на входе колебательной системы, к вызываемой ею колебательной скорости:
численно равно отношению силы F, действующей на входе колебательной системы, к вызываемой ею колебательной скорости:
![]() . (4)
. (4)
Отражение и прохождение плоских волн на границе двух сред при нормальном падении
Пусть плоская волна ![]() падает нормально на плоскую границу z=0 между двумя однородными средами. В первой среде возникает отраженная волна
падает нормально на плоскую границу z=0 между двумя однородными средами. В первой среде возникает отраженная волна ![]() , а во второй — прошедшая
, а во второй — прошедшая ![]() .
.
Мы увидим сейчас, непосредственно произведя расчет, что отражение и прохождение всегда правильные. Отраженную и прошедшую волны можно записать в виде
![]() ,
, ![]() ,
,
где ![]() и
и ![]() определяются свойствами сред и не зависят от формы волны. Для гармонических волн падающую, отраженную и прошедшую волны можно записать в виде
определяются свойствами сред и не зависят от формы волны. Для гармонических волн падающую, отраженную и прошедшую волны можно записать в виде
![]() ,
, ![]() ,
, ![]() .
.
Величины коэффициента отражения ![]() и коэффициента прохождения
и коэффициента прохождения ![]() нужно подобрать так, чтобы были удовлетворены граничные условия. Граничных условий два: равенство давлений и равенство скоростей частиц по обе стороны границы. Со стороны первой среды берется суммарное поле падающей и отраженной волны, со стороны второй — поле прошедшей волны.
нужно подобрать так, чтобы были удовлетворены граничные условия. Граничных условий два: равенство давлений и равенство скоростей частиц по обе стороны границы. Со стороны первой среды берется суммарное поле падающей и отраженной волны, со стороны второй — поле прошедшей волны.
Условие равенства давлений по обе стороны границы, или, что то же, непрерывность давления при переходе через границу, реально выполняется всегда. Нарушение этого условия вызвало бы бесконечное ускорение границы, так как сколь угодно тонкий слой сколь угодно малой массы, включающий внутри себя границу, находился бы тогда под действием конечной разности давлений по обеим сторонам слоя. В результате разность давлений выровнялась бы мгновенно.
Условие равенства скоростей выражает неразрывность среды на границе: среды не должны отдаляться друг от друга или проникать взаимно друг в друга. Это требование может на практике оказаться нарушенным, например, при кавитации, когда внутри жидкости образуются разрывы (разрывы возникают легче на границе двух сред, чем внутри одной среды). Будем считать, что нарушения граничных условий не происходит. В противном случае нижеследующий расчет неприменим, а отражение и прохождение окажутся неправильными.
Скорости частиц в падающей, отраженной и прошедшей волнах даются формулами
![]() ,
, ![]() ,
, ![]() .
.
Граничные условия можно написать так:
при ![]() ,
, ![]() ,
, ![]() .
.
Подставляя сюда соответственные выражения для давлений и скоростей частиц, найдем, сокращая на p(t):
--> ЧИТАТЬ ПОЛНОСТЬЮ <--