На рисунке проиллюстрирован случай, когда высокое значение коэффициента по Пирсону обусловленным единственной «выпадающей» точкой (выделена кружком). Показана линейная регрессия с учетом этого образца (тонкая верхняяя линия) и без него (толстая нижняя линия) [9].

Более рационально использование ранговых методов— вычисления коэффициента корреляции Кендалла (для порядковых переменных/шкал) или коэффициента корреляции Спирмена — непараметрического аналога коэффициента Пирсона для интервальных и порядковых переменных, не подчиняющихся нормальному распределению. Коэффициент Пирсона равен 1 (или минус 1) тогда и только тогда, когда две переменные (х и у) связаны линейной зависимостью (у=в+ах). Коэффициент Спирмена (или Кендалла) равен 1, если две переменные связаны правилом: большему значению переменной х всегда соответствует большее значение переменной у. Чем ниже коэффициент корреляции, тем сильнее отклонение от этих правил [9].

Следует помнить, что наличие корреляции двух переменных не означает их причинно-следственнойсвязи [8].

Существуют следующие способы сравнения двух групп по количественным признакам: вычисление доверительного интервала для разности средних или проверка гипотез (параметрическими или непараметрическими методами). В случае соответствия нормальному закону распределения переменных в каждой группе сравнение групп проводится по критериям Стьюдента (статистический модуль Basic Statistics/Tables). В противном случае - использовать непараметрические критерии, которые находятся в модуле Nonparametrics [5].

При сравнении более двух групп по количественным признакам используют однофакторный дисперсионный анализ (параметрический или непараметрический) в случае независимых групп и непараметрический метод Фридмена в случае зависимых групп. Для сравнения групп по качественным признакам используют только непараметрические критерии.

Проблема ошибочного использования методов сравнения, предназначенных для несвязанных (независимых групп), к зависимым группам отчасти решается структурой таблиц данных (размещение результатов последовательных измерений (принадлежащих к зависимым группам) в строках, а независимых—в столбец в соответствии со столбцом, содержащим код группы (Indep. (grouping) variable)). Более того, в программе пиктограммы, сопровождающие названия методов анализа носят характер подсказки: показано взаимное расположение сравниваемых массивов данных (рис.4).

Рис. 4—Список инструментов анализа с пиктограммами в модуле непараметрических методов.

При интерпретации результатов при отсутствии достоверных различий ошибочным является заключение об их отсутствии, и может быть принято только заключение о том, что различия именно не были выявлены, хотя могут и присутствовать (характерно для выборок малой численности). С другой стороны, особенно на больших выборках могут быть выявлены различия, не имеющие биологического или медицинского значения. И наоборот, даже существенное различие, выявленное при сравнении небольших групп, имеющее клиническое значение, но не быть при этом статистически значимым. Если в ходе исследования, включающего несколько больных в терминальном состоянии, хотя бы один из участников в какой-либо из групп выживет, такой результат будет клинически значимым, хотя статистически значимое различие в частоте выживания между группами может отсутствовать [11].

При проведении анализа данных часто возникает так называемая проблема множественных сравнений (ПМС), заключающаяся в следующем: чем больше статистических гипотез проверяется на одних и тех же данных, тем более вероятна ошибка первого рода — заключение о наличии различий между группами, в то время как на самом деле верна нулевая гипотеза об отсутствии различий. Так, если за уровень значимости принято значение р =0,05, то 5 из 100 вычисленных значений р в силу случайности (по теории вероятности) окажется меньше 0,05 (хотя на самом деле верна нулевая гипотеза об отсутствии различий). На практике принято считать, что учет ПМС следует начинать в тех случаях, когда число рассчитываемых значениий более 10).

В STATISTICA для уменьшения влияния множественных сравнений можно установить р на уровне 0,01 или 0,001 вместо 0,05. Считается, что такая поправка в достаточной мере компенсирует множественные парные сравнения, когда таковых избежать не удается:

1. При вторичном анализе данных.

2. При множественных парных сравнениях групп и подгрупп (по демографическим и клиническим характеристикам, исходам, временным точкам и т.д.).

3. При установлении эквивалентности групп в начале нерандомизированного исследования вмешательства.

4. При промежуточном анализе данных, полученных в испытаниях тех или иных вмешательств [7].

Анализ времени жизни в ППО STATISTICA

Данные времени жизни имеют две характерные особенности, которые предопределяют специфику их анализа. Прежде всего возможна неполнота данных. Например, в клинических исследовании больные по тем или иным причинам «уходят» из-под наблюдения, часть лабораторных животных может регулярно забиваться для проведения анализов. Реальное же время жизни таких объектов больше длительности наблюдения за ними. Описанный феномен называется цензурированием справа. Наличие цензурированных данных затрудняет оценку эффекта изучаемого воздействия на время жизни, особенно при характеристике отдаленных результатов лечения. Другая особенность данных времени жизни - неадекватность распределения времени жизни статистической модели нормального закона распределения. Конкретный же вид распределения, как правило, неизвестен. Поэтому аппроксимация распределения времени жизни нормальному закону, явная или неявная (при использовании параметрических методов анализа), представляет угрозу для корректности статистических выводов [7,8,9,10].

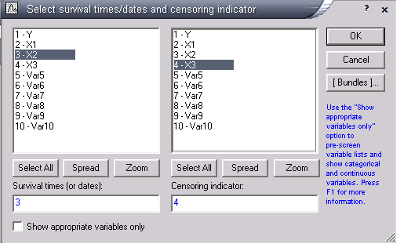
Рис.5—Диалоговое окно в анализе исхода Каплана-Майера.

Как показано на рисунке 5, ППО STATISTICA запрашивает данные о цензурированности (необходим индикатор, указывающий на значение времени (даты) исхода).

Сравнение коэффициентов корреляции

Иногда исследователи сталкиваются с проблемой сравнения нескольких коэффициентов корреляции. Так, иногда различия между двумя коэффициентами кажутся очевидными, но при этом не являются статистически значимыми, что в первую очередь может быть обусловлено различием в численности выборок [6].

ППО STATISTICA позволяет автоматически сравнить 2 коэффициента корреляции в Difference test (рис. 6). Достаточными данными являются сами коэффициенты корреляции и численности групп.

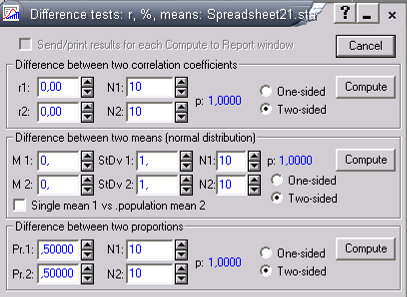
Рис.6—Инструмент «Тест различий» в модуле основной статистики

Практическая часть

В эксперименте была изучена экспрессия CD25 (рецептор к интерлейкину 2) на CD4+ лимфоцитах больных рассеянным склерозом при пролиферативном ответе на МОГ (антиген миелина). Данные получены с помощью проточного цитофлуориметра.

Принята нулевая гипотеза: Процентное содержание пролиферирующих (делящихся) клеток не связано с процентным содержанием CD25-позитивных CD4+ лимфоцитов.

Статистическая обработка данных эксперимента проведена непараметрическими методами в ППО STATISTICA 8.0. В примере приведена вторичная обработка данных с целью показать необходимость последовательного анализа, включая проверку распределения на соответствие закону нормального распределения.

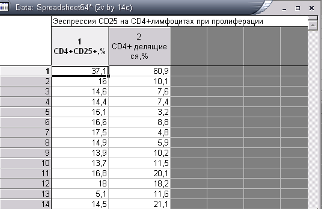
Рис. 7—Анализируемые данные