Реферат: Вписанные и описанные окружности в треугольниках и четырехугольниках

Площадь параллелограмма

Площадь параллелограмма равна произведению его основания на высоту:

Площадь параллелограмма равна произведению двух соседних его сторон ​на синус угла между ними:

Площадь треугольника

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними:

Площадь треугольника равна половине произведения его основания на высоту:

Площадь прямоугольного треугольника равна половине произведения его катетов:

Если высоты двух треугольников равны, то их площади относятся как основания.

Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы:

Площадь трапеции

Площадь трапеции равна произведению полусуммы её оснований на высоту:

Прямоугольный треугольник

Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой:

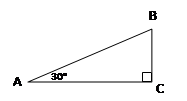
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы:

Задачи:

Задача 1: окружность, вписанная в равнобедренный треугольник, касается его боковых сторон в точках K и A. Точка K делит сторону этого треугольника на отрезки 15 и 10, считая от основания. Найдите длину отрезка KA.

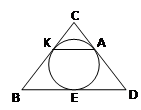
Дано: ∆ BCD – равнобедренный, K є BC, A є DC, BK = 15, KC = 10

Найти: KA

Решение: