Реферат: Вписанные и описанные окружности в треугольниках и четырехугольниках

CK = CA = 10 (отрезки касательных, проведенные из одной точки), CB = CD, следовательно AD = CD – CA, AD = 25 – 10 = 15

BE = BK = 15, DE = DA = 15 (отрезки касательных, проведенные из одной точки), следовательно BD = 15 + 15 = 30

∆ CKA ~ ∆ CBD (ﮮC – общий, CK : CB = CA : CD), следовательно KA : BD = CA : CD, KA : 30 = 10 : 25, KA = 10 ∙ 30 : 25 = 12

Ответ: KA = 12

Задача 2: Около равнобедренного треугольника с основанием AC и углом при основании 75˚ описана окружность с центром O. Найдите ее радиус, если площадь треугольника BOC равна 16.

Дано: ∆ ABC – равнобедренный, AC – основание, ﮮ ACB = 75˚,

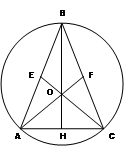площадь ∆ BOC равна 16

Найти: радиус описанной окружности

Решение:

Проведем медианы AF, CE, BH

∆ ABC – равнобедренный, BH – медиана, следовательно, BH – высота, а значит ∆ HBC – прямоугольный

ﮮ HBC = 90˚ - ﮮ ACB, ﮮ HBC = 90˚ - 75˚ = 15˚

BO = OC = R, следовательно, ∆ BOC – равнобедренный, значит ﮮHBC = ﮮECB = 15˚

ﮮ COB = 180˚ - (ﮮ HBC + ﮮECB), ﮮ COB = 180˚ - (15˚ + 15˚) = 150˚

S = ∙ BO ∙ OC ∙ sin ﮮ BOC (теорема о площади треугольника), SBOC = ∙ R ∙ R ∙ sin 150˚ = ∙ R ∙ R ∙ = ∙ R2 ; ∙ R2 = 16; R2 = 16 : = 64; R = = 8

Ответ: R = 8

Задача 3: периметр прямоугольного треугольника равен 72 м, а радиус вписанной в него окружности – 6 м. Найдите диаметр описанной окружности.

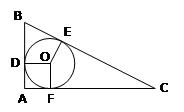Дано: ∆ ABC – прямоугольный, P = 72 м, r = 6 м

Найти: BC

Решение:

DO = OF = OE = r = 6 м, следовательно AD = AF = 6 м

FC = EC, BD = BE (отрезки касательных, проведенные из одной точки)

Пусть BD = x, FC = y, тогда AB = x + 6, AC = y + 6, BC = x + y

По теореме Пифагора AB2 + AC2 = BC2

P = AB + BC + AC, P = x + 6 + x + y + y + 6 = 2x + 2y + 12

2x + 2y + 12 = 72

(x + 6)2 + (y + 6)2 = (x + y)2

2x + 2y = 60 I: 2

x2 + 12x + 36 + y2 + 12y + 36 = x2 + 2xy + y2