Реферат: Выбор оптимального места строительства очистного сооружения

o Если , то и переход к шагу 2.

o Иначе и останов.

1.4 Метод сопряжённых градиентов

Метод сопряженных градиентов — метод нахождения локального минимума функции на основе информации о её значениях и её градиенте. В случае квадратичной функции в минимум находится за n шагов.

Определим терминологию:

Пусть .

Введём на целевую функцию.

Вектораназываются сопряжёнными , если:

·

·

где — матрица Гессе.

Теорема (о существовании). Существует хотя бы одна система сопряжённых направлений для матрицы , т.к. сама матрица (её собственные вектора) представляет собой такую систему.

1.4.1 Обоснование метода

Нулевая итерация

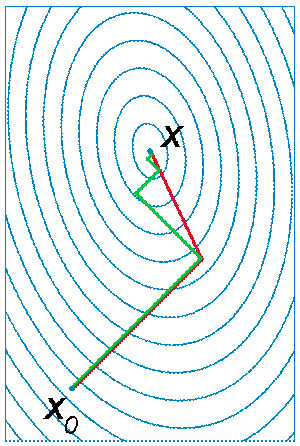
Рисунок 2 - Иллюстрация последовательных приближений метода наискорейшего спуска (зелёная ломаная) и метода сопряжённых градиентов (красная ломаная) к точке экстремума.

Пусть

Тогда .

Определим направление так, чтобы оно было сопряжено с :

Разложим в окрестности и подставим :

Транспонируем полученное выражение и домножаем на справа:

В силу непрерывности вторых частных производных. Тогда:

Подставим полученное выражение в (3):

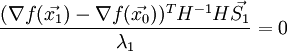
Тогда, воспользовавшись (1) и (2):

Если , то градиент в точке перпендикулярен градиенту в точке , тогда по правилам скалярного произведения векторов:

Приняв во внимание последнее, получим из выражения (4) окончательную формулу для вычисления :

[править]К-я итерация