1. Задается начальное приближение x ₀ .

2. Пока не выполнено условие остановки, в качестве которого можно взять или (то есть погрешность в нужных пределах), вычисляют новое приближение: .

2. Решение задачи в Mathcad 14

2.1 Первый способ - Сопряженный градиент

Начальное приближение

Функция Minimize ищет минимум Функции методом сопряженного градиента

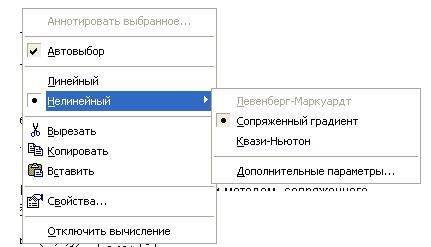
Таким образом координаты оптимального места строительства очистного сооружения

Х=4.585, У=5.654 дают минимум затрат R=23890

2.2 Второй способ - Квази-Ньютон

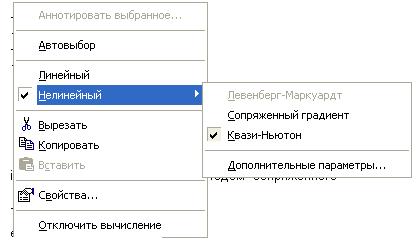
При разных дополнительных параметрах. Результат одинаков

Дает такой же ответ

Таким образом координаты оптимального места строительства очистного сооружения

Х=4.585, У=5.654 дают минимум затрат R=23890

Заключение

Были рассмотрены градиентные методы нахождения экстремумов функции :

1. Метод Ньютона,

2. Сопряженных градиентов,

3. Покоординатного спуска (Гаусса—Зейделя),

4. Скорейшего спуска( метод градиента)

Была решена задача нахождения координат очистительного предприятия исходя из условия достижения минимум затрат градиентными методами – Ньютона и сопряженных градиентов. Таким образом, координаты оптимального места строительства очистного сооружения

Х=4.585, У=5.654 дают минимум затрат R=23890

Список использованной литературы

1. Акулич И.Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. спец. вузов. — М.: Высш. шк., 1986.

2. Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. — М.: Мир, 1985.

3. Коршунов Ю.М., Коршунов Ю.М. Математические основы кибернетики. — М.: Энергоатомиздат, 1972.

4. Максимов Ю.А.,Филлиповская Е.А. Алгоритмы решения задач нелинейного программирования. — М.: МИФИ, 1982.

5. Максимов Ю.А. Алгоритмы линейного и дискретного программирования. — М.: МИФИ, 1980.

6. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1970. — С. 575-576.

7. http://ru.wikipedia.org