Реферат: Выборки и их представления

Распечатаем гистограмму.

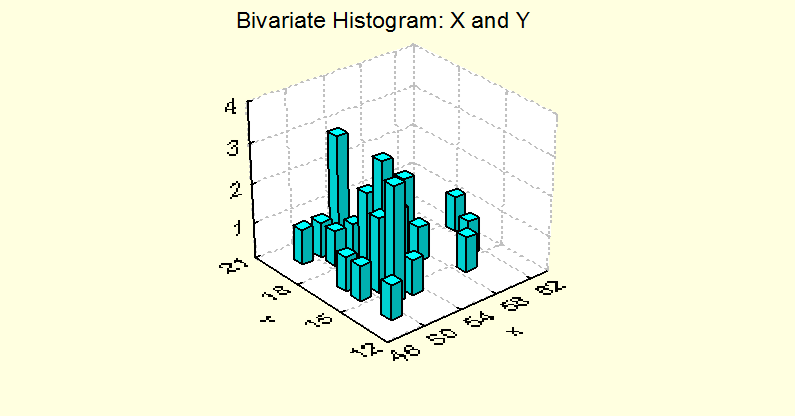
Рис. 6. Двумерная гистограмма.

4.Выполнение в пакете SPSS

Предварительно отметим:

1) диалоги заканчиваются нажатием кнопок ОК, Define или Continue для исполнения или Cancel для отмены;

2) кнопка со стрелкой (треугольником) означает перемещение выбранного элемента из одного списка в другой в направлении стрелки.

Генерация выборки

Сгенерируем 2 выборки с заданными законами распределения, например, выборки объема n = 50 c нормальным законом распределения со средним 5 и стандартным отклонением 1 и показательным (экспоненциальным) законом со средним 5.

Заготовим таблицу с 2 столбцами и n = 50 строками:

на экране таблица с пустыми клетками; прокрутим ее до 50-й строки и выделим клетку во 2-м столбце - введем любой символ, например, точку - Enter. Таблица 50 ´ 2 образована.

Создадим соответствующий файл на диске в D:\TMP:

File - New - Data - на вопрос save ...? отвечаем Yes - в окне Save As Data File : Name : D:\TMP WORK. SAV (например) - ОК.

Присвоим переменным удобные имена х1 и х2:

выделим первый столбец, кликнув мышью по заголовку - Data - Define Variable ...(определение переменной) - Variable Name: x1 - OK .

Аналогично - второй столбец.

Сгенерируем выборку с нормальным распределением:

Transform (преобразование) - Compute (вычислить) - в поле Target Variable (выходная переменная - столбец) введем имя переменной, в которую будет занесен результат: х1 ; в списке Functions выделим NORMAL (stddev) (standart deviation - стандартное отклонение), перенесем в поле Numeric Expression (вычисляющее выражение): NORMAL (1) + 5 - OK - Change...? - OK .

Сгенерируем в х2 выборку с показательным распределением со средним 5: действия аналогичны предыдущим, однако, Numeric Expression :

- 5 * LN (UNIFORM (1)),

поскольку случайная величина - a ln x ,, где x ~ R [0, 1], имеет показательное распределение со средним а ; оператор UNIFORM (x) генерирует равномерно на [0, x ] распределенные случайные числа.

Посмотрим выборку графически:

Graphs - Line - выберем Simple (простой), в поле Data in Chart Are (данные для графика) выберем Values of individual cases (значения отдельных наблюдений) - Define - â появившемся окне Define Simple из левого списка переместим кнопкой - стрелкой х1 в поле Line Represent - OK .

Наблюдаем график; его можно отредактировать (кнопка Edit ); сохраним его:

File - Save As - Name: Fig1.cht . (например) - ОК

или распечатаем: File -Print...

Посмотрим выборку х2 : действия аналогичны.

Сохраненные графики можно посмотреть еще раз:

File - Open - Chart ... - в поле Files: выделим Fig1 - OK.

Построение вариационного ряда

Data - Sort Cases... - в поле Sort by: x1 (переносом из левого списка), в поле Sort Orden: Ascending (возрастание, в отличие от Descending - сортировка по убыванию) - ОК. Сортировка проводится по указанной переменной - столбцу х1 , но сразу для всех столбцов.

Построение графика функции эмпирического распределения

Сначала построим график для выборки х1:

Statistics - Summarize - Frequencies ...- в поле Variable(s): x1 , отметим Display frequency tables (показ таблицы частот) - ОК . В окне Output (выход - окно результатов и протокола работы) появляется таблица, первый столбец которой Value (значение) - вариационный ряд, пятый - Cum. Percent (накопленные частоты в процентах) - соответствующие значения функции эмпирического распределения в процентах. Переносим столбец Value в таблицу WORK:

выделяем столбец Value (если в столбце Value имеются пустые клетки, следует выделить соответствующие строки и их удалить) - Edit - Copy (копирование в буфер) - выделяем в таблице WORK первый справа свободный столбец: Var - Edit - Past (вставить) - получаем новый столбец с вариационным рядом. Для удобства присвоим ему имя х1 v (например) (выполнение см. выше).

Аналогично переносим столбец Cum. Percent и назовем его F (например). Строим график: Graphs - Scatter...- Simple - Define - Yaxis: F, X Axis: x1v - OK - Edit - кнопка * в окне Markers (метки) выберем точку , Apply All - закроем окно Markers - кнопка и линии (в виде зигзага) - выберем Left step (левые ступеньки), Apply All - Close.

Наблюдаем функцию эмпирического распределения; сохраняем график или распечатываем.

Аналогично строим функцию эмпирического распределения для выборки х2 . Сравниваем эти две функции.

Построение гистограммы частот

Построим гистограмму для выборки х1: Graphs - Histogram...- Variable: x1 - OK . Наблюдаем гистограмму; сохраним ее или распечатаем.

Аналогично - для х2 .

Определение выборочных характеристик

Statistics - Summarize - Descriptives...- Variable(s): x1, x2, убираем выделения внизу - Options - отмечаем нужное: Mean, Sum, Std. Deviation (стандартное отклонение), Range (размах), Minimum, Maximum - Continue - OK.

Наблюдаем таблицу, в которой показаны отмеченные характеристики для обеих выборок. Выделяем таблицу и сохраняем ее:

File - Save As - Name: Descr. Lst (например) - ОК . Сравниваем выборочные средние и стандартные отклонения с теоретическими.

Проверка гипотезы о типе распределения

Проверим обе наши выборки с помощью критерия Колмогорова - Смирнова на нормальность распределения и равномерность:

Statistics - Nonparametric Tests - 1 Sample K - S - в поле Test Variable List: x1, x2 (переносом из списка слева), в поле Test Destribution отметим Normal, Uniform - OK.

В окне Output даются результаты тестирования двух выборок по двум гипотезам: итого 4 сообщения. Например, результат тестирования х1 на нормальность (Test distribution - Normal ): приводятся параметры гипотетического распределения (оценки) Mean è Standart Deviation ; статистика Dn Колмогорова (Most estreme differences Absolute ), z = Dn (K – S Z) и уровень значимости 2 – Tailed P ; если последний порядка сотых долей или меньше, гипотезу следует отклонить.

Выписываем упомянутые значения и делаем выводы.

Заметим, что такой способ проверки при отклонении гипотезы можно считать корректным, а при принятии - это не совсем так (см. более подробные руководства по статистике).

Описание двумерных выборок

а) Ввод данных: в свободные два столбца введем с клавиатуры данные из табл. 2; назовем их x и y.

б) Диаграмма рассеяния:

Graphs - Scatter...- Simple - Define - X Axis: x, Y Axis: y - OK .

Наблюдаем диаграмму; сохраним ее или распечатаем.

в) Выборочные характеристики.

Некоторые характеристики см выше.

Определение корреляционной матрицы:

Statistics - Correlate - Bivariate - в поле Variables: x, y (переносом из левого списка), Correlation Coefficients : Pearson Test of Significance: Two - tailed (двусторонний тест Пирсона на значимость отличия от нуля) - ОК .

В окне Output имеем таблицу 2 ´ 2 коэффициентов корреляции и уровней значимости Р ; если Р порядка сотых долей или меньше, гипотезу о нулевом значении коэффициента следует отклонить. Если Р порядка 0.1 или более, коэффициент корреляции следует считать нулевым. Матрицу выделяем и сохраняем ее или распечатываем.

г) Трехмерная диаграмма.

Для примера образуем третью переменную (столбец) z , равную x + y.

Построим диаграмму:

Graphs - Scatter...- 3D - Define - X Axis: x, Y Axis: y, Z Axis: z - OK .