Реферат: Вычисление обратной матрицы

Рассмотрим квадратную матрицу

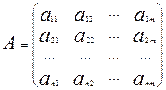
Квадратная матрица А называется невырожденной , или неособенной , если её определитель отличен от нуля и вырожденной , или особенной , если её определитель равен нулю.

Квадратная матрица В называется обратной для квадратной матрицы А того же порядка, если их произведение

АВ= ВА=Е ,

где Е – единичная матрица того же порядка, что и матрицы А и В.

Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы её определитель был отличен от нуля.

Матрица, обратная к А , обозначается через А^-1 , так что В= А^-1 . Для матрицы А обратная ей матрица А^-1 определяется однозначно.

Справедливы следующие равенства:

1) D (А^-1 )=( D А)^-1 ;

2) (А^-1 )^-1 =А ;

3) (А₁ А₂ )^-1 =А₂ ^-1 А₁ ^-1 ;

4) (А^Т )^-1 =(А^-1 )^Т .

Существую несколько способов нахождения обратной матрицы. Рассмотрим один из них – нахождение обратной матрицы путём вычисления алгебраических дополнений. Заключается он в следующем:

пусть нам дана матрица А , имеющая следующий вид:

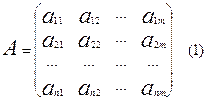
Предположим, что D А ¹ 0 . Построим следующую матрицу С следующим образом:

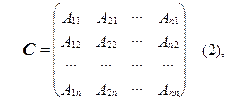
где А _ij – алгебраическое дополнение элемента а _ij в определителе матрицы А . Очевидно, что для построения матрицы С необходимо сначала заменить элементы матрицы А соответствующими им алгебраическими дополнениями, а затем полученную матрицу транспонировать.

Полученная таким образом матрица С называется присоединённой к матрице А , или союзной с А .

Чтобы получить матрицу А^-1 , обратную для матрицы А , необходимо каждый элемент присоединённой матрицы С поделить на D А , т.е. матрица А^-1 будет иметь следующий вид:

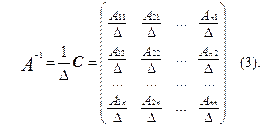
Пусть матрица А , имеет следующий вид:

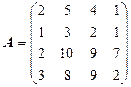
Чтобы найти матрицу А^-1 , обратную для матрицы А , необходимо:

- вычислить определитель матрицы (D А= -3 );

- найти алгебраические дополнения элементов а _ij в определителе матрицы А :

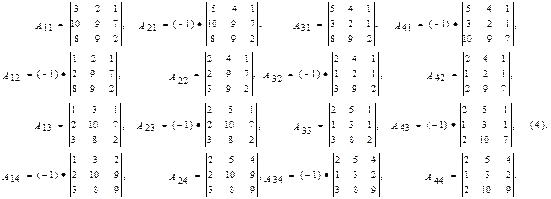
- составить присоединённую матрицу С по формуле (2);

- разделить все элементы матрицы С на D А .

Реализуем вышеизложенный алгоритм нахождения обратной матрицы следующим образом: вначале запишем в редакторе Word присоединенную матрицу С по формуле (2), после чего в программе Excel найдём обратную матрицу А^-1 (по формуле (3)) для матрицы А .

1. Включите компьютер.

2. Подождите пока загрузится операционная система Windows , после чего откройте окно Microsoft Word .

3. Вставьте объект Microsoft Equation 3 . 0.

4. Перепишем алгебраические дополнения в формульный редактор. Для этого:

·запишите алгебраическоедополнение А₁₂ ., используя шаблон нижних индексов;

--> ЧИТАТЬ ПОЛНОСТЬЮ <--