Реферат: Выполнение операций алгебраического сложения и сдвига в ЭВМ

А_пр =0,101101 В_пр =1,000111

А_дк =0,101101 В_ДК =1,111001 С_дк =А_дк +В_дк

₊ 0,101101

1,111001

1¬0,100110 (1 переноса из знакового разряда суммы не учитывается)

3) ??0, ›0, ы0.

А=-0,101101 В=+0,000111

А_пр =1,101101 В_пр =0,000111

А_дк =1,010011 В_ДК =0,000111 С_дк =А_дк +В_дк

₊ 1,010011

0,000111

1,011010 (С_пр = 1,100110)

4) ??0, ‹0, ы0.

А=-0,101101 В=-0,000111

А_пр =1,101101 В_пр =1,000111

А_дк =1,010011 В_ДК =1,111001 С_дк =А_дк +В_дк

₊ 1,010011

1,111001

1¬1,001100 (С_пр = 1,110100)

При сложении в дополнительном коде возможно переполнение разрядной сетки (в первом и четвертом случаях). Признаком переполнения является отличие знака полученной суммы от знаков слагаемых.

1.1.5 Обратный код

Числа в обратном коде представляются в следующем виде для двоичных чисел:

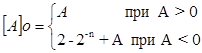
Обратный код положительного числа совпадает с его представлением в прямом коде. Обратный код отрицательного числа получают инвертированием всех разрядов числа, кроме знакового.

[A]_пр =0,10110100; [A]_ок =0,10110100;

[В]_пр =1,10111101; [В]_ок =1,01000010.

1.1.6 Сложение в обратном коде

В обратном коде, как и в дополнительном, операция вычитания заменяется операцией сложения. При этом знаковый разряд и цифровая часть числа рассматриваются как единое целое. Правильный знак суммы получается в результате суммирования цифр знаковых разрядов операндов и единицы переноса из цифровой части, если она есть. Характерной особенность сложения в обратном коде является наличие циклического переноса (если он возникает) из знакового разряда в младший разряд цифровой части, благодаря которому осуществляется коррекция суммы на 2^{- n} .

Рассмотрим все возможные варианты сложения чисел в обратном коде:

1) ??0, ›0, ћ0.

А=+0,101101 В=+0,000111