Реферат: Высокотемпературная сверхпроводимость 2

Із-за малої довжини когерентності x»( 1-30 )A вихрі слабо закріплені на дефектах зразка і можуть легко переміщатися по ньому як і при пропусканні через зразок струму, так і при наявності інгрідієнта температури. Рис.1.13 служить якісною ілюстрацією механізма руху вихрів. Потенціальний рельєф для вихрів у зразку визначає силу пінінга (рис.1.13 а).

Рис.1.1.3. Схематичне зображення потенціального рельєфу, який призводить до пінінгу і його зміна при протіканні струму через зразок.

Якщо через зразок пропускати струм, то із-за сили Лоренца [ J´B ], яка діє на вихрі потенціальний рельєф зміниться (рис.1.1.3 б і в). При критичному струмові J_c всі вихві починають вільно рухатись по зразку, тобто пінінг в цьому випадку відсутній. Однак при кінечній температурі існує ймовірність руху вихрів і при J< J_c . Дійсно, ймовірність проникнення вихрів через бар’єр висотою U

W = W₀ exp ( -U / kT ). (1.1.1)

При наявності струму

U = U₀ ( 1 - J / J_c ), (1.1.2)

і тому

(1.1.3)

Вирішуючи цей вираз відносно J, отримуємо

. (1.1.4)

Таким чином, якщо в надпровіднику ІІ роду з пінінгом можливий надпровідний струм, то він буде затухати з часом. В традиційних надпровідниках U₀ /kT велике, і цей ефект практично відсутній. В ВТНП величина U₀ /kT»0,1, і рух вихрів легко спостерігати.

Цей ефект легко спостерігається шляхом вимірювання часової залежності встановлення стану рівноваги магнітного моменту після різкої зміни зовнішнього магнітного поля або температури. Швидкість релаксації намагнічення в ВТНП може коливатись від декількох секунд до десятків годин в залежності від температури.

Перші ВТНП були отримані спіканням відповідних хімічних елементів з послідуючим відпалом в атмосфері кисня. В результаті отримується керамічний сплав, який складається з спечених гранул. Тому такі ВТНП називають керамічними або гранулярними. Характерний розмір складає біля 10 мкм. Перші експеременти проводились саме на таких керамічних зразках, і лише потім навчилися вирощувати монокристалічні зразки, що до цього є досить важкою технологічною задачою. Гранулярні надпровідники представляють собою середовище з слабкими джозефсоновськими зв’язками, які визначають незвичайні його електродинамічні властивості.

1 .2. НВЧ властивості плівок ВТНП.

Основою феноменологічної моделі, котра широко застосовується при розрахунках поверхневого опору на НВЧ, є двухрідинна модель надпровідника. В рамках цієї моделі зв’язок струму і поля має вигляд

(1.2.1)

де

, , (1.2.2)

n_N i n_S - концентрація носіїв при Т<T_c .

Для полів, які міняються по гармонічному закону, використання рівнянь Максвела разом з (1.2.1-1.2.2) дозволяє ввести ефективну діелектричну проникність середовища

. (1.2.3)

Тут e^¢ - відносна діелектрична проникність кристалічної гратки; l_L - лондонівська глибина проникнення [ 14 ]. Для аналізу електродинаміки надпровідника потрібно визначити хвильвий опір W i хвильове число k для плоскої хвилі, яка розповсюджується в надпровіднику. В випадку розповсюдження хвилі в вакуумі , .

Підставляючи сюди замість e₀ співвідношення (1.2.3) для e_eff і опускаючи в ньому член, який містить e^¢ , отримаємо

; , (1.2.4)

де

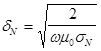. (1.2.5)

Величина d має зміст комплексної глибини проникнення, а d_N - скінової глибини, яка пов’язана з наявністю носіїв у вільному стані. Замітимо, що побудована модель справедлива в області частот w<w_кр , де - критична частота, яка визначається співвідношенням hw_кр =2D. Тут 2D - енергія носіїв заряда, які знаходяться в s-стані. Для ВТНП-матеріалів w_кр =10¹³ ¸10¹⁴ с^-1 і лежить значно вище частот НВЧ-діапазону.

Приведені співвідношення дають повну характеристику двохрідинної моделі надпровідника з точки зору макроскопічної електродинаміки. Від фізики надпровідності вимагається вказати температурні залежності величин d_N і l_L .

Нажаль, в наш час не існує ні строгих теоретичних доведень, ні надійних експерементальних даних відносно цих параметрів. Допустимо, що носії заряду в ВТНП-матеріалів підчиняються статистиці Бозе, можуть бути описані моделлю ідеального бозе - газу і при Т=Т_с випробовують бозе - конденсацію. При цьому

, (1.2.6)