Реферат: Задача по Физике 2

№506 На тонкую пленку в направлении нормали к ее поверхности падает монохроматический свет с длиной волны l = 500 нм. Отраженный от нее свет максимально усилен вследствие интерференции. Определить минимальную толщину d_min пленки, если показатель преломления материала пленки n = 1,4.

Дано: Решение:

l = 500 нм= В условии не указано, что пленка нанесена на стеклянную

=500*10^{-9 м} пластину. Поэтому оптическая разница хода световых волн,

n = 1,4 возникающая при отражении монохроматического света от

d_min - ? от тонкой пленки: Δ=2dncosi₂ +λ/2 (1), где

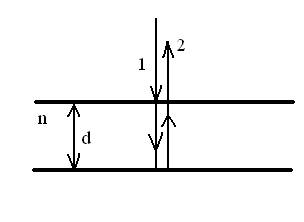
d – толщина пленки;

n – показатель преломления;

i₂ – угол преломления света в пленке, i₂ =0;

λ/2 – добавочная разность хода, возникающая из-за отражения от оптически более плотной среды.

Условие максимума: Δ =kλ (2)

(1)=(2) 2dn+λ/2=kλ

2dn=(λ/2)*(2k-1)

d=(λ/4n)*(2k-1)

d_min приk=1 d_min =λ/4n=(500*10^-9 )/(4*1.4)=89,3*10^-9 м=89,3нм

Ответ: d_min = 89,3нм

№516 На дифракционную решетку, содержащую n = 100 штрихов на 1 мм, нормально падает монохроматический свет. Зрительная труба спектрометра наведена на максимум второго порядка. Чтобы навести трубу на другой максимум того же порядка, ее нужно повернуть на угол Dj = 16°. Определить длину волны l света, падающего на решетку.

Дано: Решение:

n=100 штр/мм= Условие наблюдения максимума на дифракционной решетке

=100000 штр/м dsinφ=kλ (1), где

k=2 k – порядок максимума;

Δφ=16° φ – угол дифракции.

λ - ? φ=Δφ/2 (2) – в силу симметрии максимумов

d=1/n (3) – постоянная (период решетки)

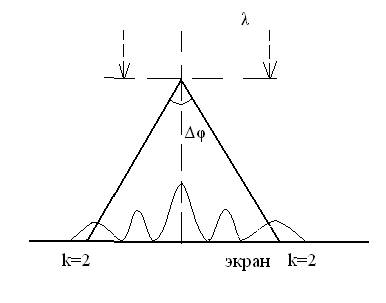
Тогда (1) перепишется: (1/n)sin(Δφ/2)= kλ (4)

λ=(1/kn)sin(Δφ/2)=(1/10⁵ *2)sin8°=6.96*10^-7 м

Ответ: λ=6.96*10^-7 м

№526. Пучок света переходит из жидкости в стекло. Угол падения i пучка равен 60°, угол преломления r = 50°. При каком угле падения i_в пучок света, отраженный от границы раздела этих сред, будет максимально поляризован?

Дано: Решение:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--