Реферат: Задачи по статистике
(11)
и показывает долю общей вариации результативного признака, обусловленную вариацией группировочного признака.
Корень квадратный из коэффициента детерминации называется эмпирическим корреляционным отношением:
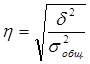
(12)
По абсолютной величине он может меняться от 0 до 1. Если 
, группировочный признак не оказывает влияния на результативный. Если 
, изменение результативного признака полностью обусловлено группировочным признаком, т.е. между ними существует функциональная связь.
Решение :
1. Интервал (по формуле (2) ):
где 
– число выделенных интервалов.
100-220; 220-340; 340-460; 460-580; 580-700
| Численность промышленно-производственного персонала, чел. | Выпуск продукции, млн. руб. | Итого | ||||
| 19,0-50,8 | 50,8-82,6 | 82,6-114,4 | 114,4-146,2 | 146,2-178 | ||
| 100-220 | 3 | 3 | ||||
| 220-340 | 4 | 4 | ||||
| 340-460 | 1 | 7 | 9 | |||
| 460-580 | 1 | 3 | 4 | |||
| 580-700 | 2 | 2 | ||||
| Итого: | 3 | 6 | 8 | 3 | 2 | 22 |
Строим рабочую таблицу распределения предприятий по численности персонала:
| № группы | Группировка | № предприятия | Численность | Выпуск |
| I | 100-220 | 8 | 100 | 19,0 |
| 2 | 170 | 27,0 | ||
| 15 | 210 | 44,0 | ||
| ИТОГО: | 3 | 480 | 90,0 | |
| В среднем на одно предприятие | 160 | 30,0 | ||
| II | 220-340 | 4 | 230 | 57,0 |
| 11 | 260 | 55,0 | ||
| 14 | 280 | 54,0 | ||
| 6 | 290 | 62,0 | ||
| ИТОГО: | 4 | 1060 | 228,0 | |
| В среднем на одно предприятие | 265 | 57,0 | ||
| III | 340-460 | 3 | 340 | 53,0 |
| 10 | 340 | 83,0 | ||
| 19 | 380 | 88,0 | ||
| 21 | 400 | 90,0 | ||
| 22 | 400 | 71,0 | ||
| 7 | 410 | 86,0 | ||
| 1 | 420 | 99,0 | ||
| 18 | 420 | 95,0 | ||
| 13 | 430 | 101,0 | ||
| ИТОГО: | 9 | 3540 | 766,0 | |
| В среднем на одно предприятие | 393,333 | 85,111 | ||
| IV | 460-580 | 16 | 520 | 94,0 |
| 9 | 550 | 120,0 | ||
| 5 | 560 | 115,0 | ||
| 20 | 570 | 135,0 | ||
| ИТОГО: | 4 | 2200 | 464,0 | |
| В среднем на одно предприятие | 550 | 116,0 | ||
| V | 580-700 | 12 | 600 | 147,0 |
| 17 | 700 | 178,0 | ||
| ИТОГО: | 2 | 1300 | 325,0 | |
| В среднем на одно предприятие | 650 | 162,5 | ||
| ВСЕГО: | 22 | 8580 | 1873,0 | |
Теперь по данным рабочей таблицы строим итоговую аналитическую таблицу:
| № группы | Группировка | Число | Численность | Выпуск | ||
| Всего | В среднем на | Всего | В среднем на | |||
| I | 100-200 | 3 | 480 | 160 | 90,0 | 30,0 |
| II | 220-340 | 4 | 1060 | 265 | 228,0 | 57,0 |
| III | 340-460 | 9 | 3540 | 393,333 | 766,0 | 85,111 |
| IV | 460-580 | 4 | 2200 | 550 | 464,0 | 116,0 |
| V | 580-700 | 2 | 1300 | 650 | 325,0 | 162,5 |
| ИТОГО: | 22 | 8580 | 390 | 1873,0 | 85,136 | |
По данным аналитической таблицы мы видим, что с приростом объема продукции, средняя численность персонала на одно предприятие возрастает.
Значит, между исследуемыми признаками существует прямая корреляционная зависимость.
2. Строим расчетную таблицу:
| № группы | Группировка | Число | Выпуск, |
|
|
| |
| Всего | В среднем | ||||||
| I | 100-220 | 3 | 50,0 | 30,0 | -55,136 | 3039,978 | 9119,934 |
| II | 220-340 | 4 | 228,0 | 57,0 | -22,135 | 791,634 | 3166,536 |
| III | 340-460 | 9 | 766,0 | 85,111 | -0,025 | 0,000625 | 0,005625 |
| IV | 460-580 | 4 | 464,0 | 116,0 | 30,864 | 952,586 | 3810,344 |
| V | 580-700 | 2 | 325,0 | 162,5 | 77,364 | 5985,188 | 11970,376 |
| ИТОГО: | 22 | 1873,0 | 85,136 | 28067,195 | |||
Вычисляем коэффициент детерминации по формуле:
где 
- межгрупповая дисперсия, находящаяся по формуле:
- общая дисперсия результативного признака, находящаяся по формуле:
Теперь находим 
Для каждой группы предприятий рассчитаем значение 
и внесем в таблицу.
Находим межгрупповую дисперсию:
