Реферат: Задачи по статистике

Вариант 2

Выполнил: Кончаков Е.А.____

3 курс, 310 гр.____________

Проверила: Каманина А.М._

г. Москва, 2001 г.

Задача №1.

Имеются следующие выборочные данные (выборка 10%-ная, механическая) по предприятиям одной из отраслей промышленности:

№ предприятия	Численность промышленно-производственного персонала, чел.	Выпуск продукции, млн. руб.	№ предприятия	Численность промышленно-производственного персонала, чел.	Выпуск продукции, млн. руб.
1	420	99,0	12	600	147,0
2	170	27,0	13	430	101,0
3	340	53,0	14	280	54,0
4	230	57,0	15	210	44,0
5	560	115,0	16	520	94,0
6	290	62,0	17	700	178,0
7	410	86,0	18	420	95,0
8	100	19,0	19	380	88,0
9	550	120,0	20	570	135,0
10	340	83,0	21	400	90,0
11	260	55,0	22	400	71,0

По исходным данным:

1. Постройте статистический ряд распределения предприятий по выпуску продукции, образовав пять групп с равными интервалами. Постройте графики ряда распределения.
2. Рассчитайте характеристики ряда распределения предприятий по выпуску продукции: среднюю арифметическую, среднее квадратическое отклонение, дисперсию, коэффициент вариации.

Сделайте выводы.

1. С вероятностью 0,954 определите ошибку выборки среднего выпуска на одно предприятие и границы, в которых будет находиться средний выпуск продукции отрасли в генеральной совокупности.

• C одержание и краткое описание применяемых методов:

Статистическая группировка в зависимости от решаемых задач подразделяются на типологические, структурные аналитические. Статистическая группировка позволяет дать характеристику размеров, структуры и взаимосвязи изучаемых явлений, выявить их закономерности.

Важным направлением в статистической сводке является построение рядов распределения, одно из назначений которых состоит в изучении структуры исследуемой совокупности, характера и закономерности распределения.

Ряд распределения – это простейшая группировка, представляющая собой распределение численности единиц совокупности по значению какого-либо признака.

Ряды распределения, в основе которых лежит качественный признак, называют атрибутивным. Если ряд построен по количественному признаку, его называют вариационным.

При построении вариационного ряда с равными интервалами определяют его число групп () и величину интервала (). Оптимальное число групп может быть определено по формуле Стерджесса:

, (1)

где- число единиц совокупности.

Величина равного интервала рассчитывается по формуле:

(2)

где – число выделенных интервалов.

Средняя – является обещающей характеристикой совокупности единиц по качественно однородному признаку.

В статистике применяются различные виды средних: арифметическая, гармоническая, квадратическая, геометрическая и структурные средние – мода и медиана. Средние, кроме моды и медианы, исчисляются в двух формах: простой и взвешенной. Выбор формы средней зависит от исходных данных и содержание определяемого показателя. Наибольшее распространение получила средняя арифметическая, как простая, так и взвешенная.

Средняя арифметическая простая равна сумме значений признака, деленной на их число:

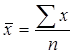, (3)

где – значение признака (вариант);

–число единиц признака.

Средняя арифметическая простая применяется в тех случаях, когда варианты представлены индивидуально в виде их перечня в любом порядке или в виде ранжированного ряда.

Если данные представлены в виде дискретных или интервальных рядов распределения, в которых одинаковые значения признака () объединены в группы, имеющие различное число единиц (), называемое частотой (весом), применяется средняя арифметическая взвешенная:

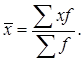
(4)

Для измерения степени колеблемости отдельных значений признака от средней исчисляются основные обобщающие показатели вариации: дисперсия, среднее квадратическое отклонение и коэффициент вариации.

Дисперсия () – это средняя арифметическая квадратов отклонений отдельных значений признака от их средней арифметической. В зависимости от исходных данных дисперсия вычисляется по формуле средней арифметической простой или взвешенной:

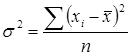- невзвешенния (простая); (5)

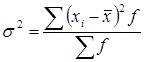- взвешенная. (6)

Среднее квадратическое отклонение () представляет собой корень квадратный из дисперсии и рано:

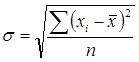- невзвешенния; (7)

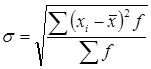- взвешенная. (8)

В отличие от дисперсии среднее квадратическое отклонение является абсолютной мерой вариации признака в совокупности и выражается в единицах измерения варьирующего признака (рублях, тоннах, процентах и т.д.).

Для сравнения размеров вариации различных признаков, а также для сравнения степени вариации одноименных признаков в нескольких совокупностях исчисляется относительный показатель вариации – коэффициент вариации (), который представляет собой процентное отношение среднего квадратического отклонения и средней арифметической:

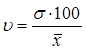
(9)

По величине коэффициента вариации можно судить о степени вариации признаков, а, следовательно, об однородности состава совокупности. Чем больше его величина, тем больше разброс значений признака вокруг средней, тем менее однородна совокупность по составу.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--